Com aprendre un nen per comptar ràpidament en la teva ment?
Els pares de nens moderns amb enveja estan veient els geeks - participants del programa de televisió "El millor de tots" i "Amazing People" - i es preocupen que els seus fills no es distingeixin per una intel·ligència excepcional i una intel·ligència: no dominen el programa de l'escola primària, no els agrada colar els cervells i tenen por de les lliçons. matemàtiques.
Des de la primera classe, compten amb dits i varetes, no saben tècniques de recompte oral, per tant, tenen grans problemes en totes les matèries del curs escolar.
Les tècniques de recompte oral ràpid són simples i es poden digerir fàcilment, però cal recordar que el seu èxit no implica un ús mecànic, sinó molt conscient de les tècniques i, a més, un entrenament més o menys llarg.
Després d'haver dominat els mètodes elementals de comptes orals, utilitzar-los podrà realitzar correctament i ràpidament els càlculs instantanis a la ment amb la mateixa precisió que amb els càlculs escrits.
Característiques
Hi ha moltes tècniques que promouen l’aprenentatge per accelerar l’aritmètica mental. Amb totes les diferències visibles, tenen una similitud important: es basen en tres "balenes":
- Formació i acumulació d'experiències. La pràctica regular, la solució de tasques de simples a complexos, canvien qualitativament i quantitativament la capacitat de computació oral.
- Algorisme. El coneixement i l'aplicació de mètodes i lleis "secretes" simplifiquen enormement el procés de comptar.
- Habilitats i dotacions naturals. Desenvolupar memòria a curt termini i el seu volum considerable, així com una alta concentració d’atenció, una gran ajuda per practicar una aritmètica mental ràpida. Un avantatge definitiu és la presència d’una mentalitat matemàtica i una predisposició al pensament lògic.
L'ús del compte oral
La gent no és un robot de ferro, però el fet de crear màquines intel·ligents parla de la seva superioritat intel·lectual. Una persona necessita mantenir el cervell constantment en bona forma, la qual cosa promou activament la formació d’habilitats en l’aritmètica mental.
Per a la vida quotidiana:
- un compte oral reeixit és un indicador d'una mentalitat analítica;
- l'aritmètica mental regular us estalviarà de la demència primerenca i del marasme senil;
- la vostra capacitat d’afegir i restar bé no us permetrà enganyar a la botiga.
Per a un estudi reeixit:
- activitat mental activada;
- desenvolupar memòria, parla, atenció, capacitat de percebre allò que es va dir a l'audiència, rapidesa de la reacció, enginy, capacitat de trobar les maneres més racionals de resoldre la tasca establerta;
- reforçar la confiança en les seves capacitats.
Quan he de començar els meus estudis?
Segons les ments científiques (psicòlegs i educadors), un nen al quart any ja és capaç d'afegir i de restar. Als 5 anys, la migdiada pot resoldre lliurement exemples i tasques senzilles. Però són estadístiques i els nens no sempre s'adapten a ella. Per tant Tot aquí és purament individual.
En qualsevol cas, és millor ensenyar als nens a comptabilitzar ràpidament la seva ment abans d'entrar a l'escola; hi haurà menys problemes i un subministrament d'habilitats útils ajudarà a dominar els programes escolars moderns amb més èxit.
Normes
La Reina de les Ciències - Matemàtiques - va tenir cura dels estudiants i va elaborar un conjunt de lleis, Algorismes i regles, que els han dominat i hàbilment, els nens els encantarà les matemàtiques i el treball mental:
- La propietat de transferència de l’addició: canviant els components de l’acció, obtenim el mateix resultat.
- La propietat d’addició combinada: quan s'afegeixen tres o més números, es poden substituir dos (o més) valors numèrics per la seva suma.
- Addició i resta amb la transició a través d'una dotzena: afegir un component més gran
- A desenes de rodons, i després afegir la resta de l’altre component.
- Primer restem les unitats individuals del nombre al signe de l’acció, i després de les desenes de rondes restem la resta del deduïble.
- Després d’haver presentat la disminució en forma de la suma de desenes i unitats, eliminem de les desenes de les més grans les més petites i afegim a la resposta les unitats de la disminució.
- Quan s’afegeixen i resten dotzenes de rondes (encara se'ls anomena números "rodons"), es poden considerar dotzenes les mateixes que les unitats.
- Suma i resta de desenes i unitats. Dotzenes més convenient per afegir a les dotzenes i unitats a les unitats.
Afegiu un número a la quantitat
Els mètodes són els següents:
- Calculem el seu valor i, a continuació, afegim el valor donat.
- L'afegim al primer terme i després afegim el segon terme al resultat.
- Afegim el número al segon terme i després afegirem el primer terme a la resposta.
L’addició de l’import al número
Els mètodes són els següents:
- Calculeu el seu testimoni i, a continuació, afegiu-lo al número.
- Afegim el primer terme al número i després afegim el segon terme al resultat.
- Afegim el segon terme al número i després afegim el primer terme al resultat.
L’addició de dues sumes. Si afegiu dues sumes, escollim la manera més convenient de calcular.
Utilitzar les principals propietats de multiplicació
Les tècniques són les següents:
- La propietat de transferència de la multiplicació. Si canviem els factors en llocs, el seu producte no canviarà.
- La propietat combinada de la multiplicació. Quan multipliqueu tres o més números, es poden substituir dos (o més) números pel seu producte.
- Propietat de distribució de la multiplicació. Per multiplicar la suma per un nombre, és necessari multiplicar cada un dels seus components per aquest número i afegir les obres resultants.
Multiplicar i dividir els números per 10 i 100
Maneres:
- Per augmentar qualsevol nombre 10 vegades, heu d’afegir un zero a la dreta.
- Per fer el mateix 100 vegades, cal assignar-li dos zeros a la dreta.
- Per reduir el nombre 10 vegades, heu de deixar un zero a la dreta i dividir per 100 - dos zeros.
Multipliqueu l’import pel número
Maneres:
- 1r mètode. Calculeu l’import i multipliqueu-lo per aquest valor.
- 2a via. Multipliqueu el número amb cadascun dels afegits i afegiu les respostes resultants.
Multipliqueu el nombre per suma
Maneres:
- 1r mètode. Cerqueu la suma i multipliqueu el nombre pel que obtenim.
- 2a via. Multipliqueu el nombre per cada un dels afegits i afegiu les obres resultants.
Divisió de l'import pel número
Maneres:
- 1r mètode. Calculeu l’import i dividiu-lo per un número.
- 2a via. Cada un dels afegits es divideix pel nombre i s'afegeixen els quocients resultants.
Dividir el nombre del producte
Opcions:
- 1r mètode. Dividiu el nombre pel primer factor i després dividiu el resultat pel segon factor.
- 2a via. Divideix el nombre pel segon factor i, a continuació, divideix el resultat pel primer factor.
Espècie
Durant les lliçons, es dóna un temps limitat al compte oral, però això no desvira la seva importància per al desenvolupament de l'activitat mental dels nens. Les habilitats computacionals orals es formen en les classes de matemàtiques a l'escola primària quan es realitzen diversos tipus de tasques i exercicis.
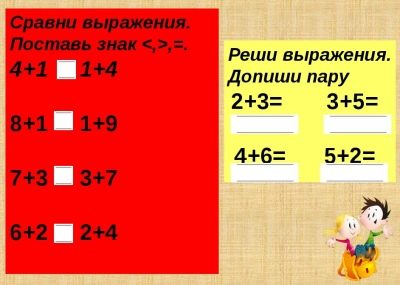
Cerqueu el valor d’una expressió matemàtica
Poden ser expressions numèriques ordinàries o expressions amb una variable (alfabètica) i es suggereixen valors numèrics per a lletres.Substituint els números en comptes de les lletres, trobeu el valor numèric de l’expressió resultant.
Compareu les expressions matemàtiques
Aquestes tasques són variades:
- determinar la igualtat o la desigualtat de les dues expressions donades (havent trobat i comparat prèviament els seus valors);
- a la relació donada al signe i a una de les expressions per compondre la segona expressió o completar la proposta inacabada;
- en aquests exercicis, els números i les quantitats de un dígit, de dos dígits, es poden utilitzar en expressions i en les quatre operacions aritmètiques. L’objectiu principal d’aquestes tasques és el domini del material teòric i el desenvolupament d’habilitats computacionals sòlides.
- Resoldre l’equació. Ajuden a entendre les relacions entre els components i els resultats de les operacions aritmètiques.
- Resol el problema. Pot ser tasques senzilles i complexes. Amb la seva ajuda, es reforcen els coneixements teòrics, es desenvolupen habilitats computacionals i habilitats, s'activa l’activitat mental dels nens.
Recepcions de comptes orals
Signes de divisibilitat dels números:
- per 2: tots els que la superen, i en les sèries numèriques passen per una;
- a 3 i 9: si la suma dels dígits és múltiple d'aquests indicadors sense un equilibri;
- per 4: si els dos últims dígits del registre formen successivament un nombre dividit per 4;
- 5: rodons de dotzenes i aquells en què hi ha 5 al final;
- per 6: els números que són múltiples de dos i tres es divideixen;
- 10: els valors numèrics, en què el registre és al final és 0;
- 12: dividiu els números que es poden dividir en tres i quatre alhora;
- per 15: els números que es divideixen simultàniament per components sencers d’un únic valor d’aquest nombre són multiplicadors.
Formularis de comptes de l'escola primària
És ben sabut que l’activitat principal dels preescolars i dels estudiants més joves és un joc útil per incloure-ho en totes les etapes de la lliçó. A continuació es donaran algunes formes del compte oral.
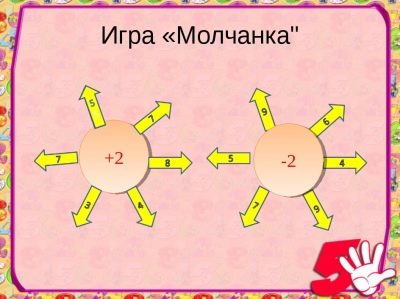
El joc "Silent"
Ajuda a fomentar l'atenció i la disciplina. Un silenci pot consistir en exemples en una acció, dos o més. Es juga a totes les classes de l’escola primària amb tots dos enters abstractes i nombres nomenats.
Els estudiants consideren en la seva ment i en silenci a la trucada que els professors escriuen les respostes als exemples que se'ls ofereixen a la pissarra. Les respostes correctes es donen amb claves clares i les respostes equivocades amb silenci.
Joc "Lotto"
Pot haver-hi diversos tipus corresponents a aquelles seccions de matemàtiques que s’estudien i necessiten ser arreglades. Per exemple, loteria amb exemples de multiplicació i divisió dins dels "centenars".
Per donar més interès al joc, els pneumàtics amb respostes es poden fer a partir d’una imatge retallada. Si tots els exemples es resolen correctament, es fa una imatge dels pneumàtics.
Joc "laberints aritmètics"
Semblen cercles concèntrics amb portes amb números. Per arribar al centre, cal marcar un número al centre. Els laberints de la solució poden requerir una acció (addició) o diverses. Cal assenyalar que aquestes tasques tenen diverses solucions.
El joc "Captura el pilot" (una mena de "escala")
Al tauler de dibuix: un pla amb bucles, en què exemples. Dos estudiants convocats registren respostes a l'esquerra i a la dreta dels bucles. Qui decideix correctament i ràpidament, es posarà al dia amb el pilot.
El joc "Exemples circulars"
El material didàctic és un conjunt de targetes disposades en sobres; Cadascun d'ells té 8 cartes, cadascuna de les quals conté un exemple.
Els exemples numèrics de cada sobre tenen un contingut diferent i es seleccionen segons el principi de l'autocontrol: en resoldre'ls, el resultat d’un exemple serà el començament de la següent.
Es poden oferir exemples circulars com a escales.
Mètodes i tècniques de desenvolupament
Tenint en compte les maneres d’ensenyar als nens de 6 anys a comptar amb rapidesa en la seva ment, és impossible no tenir en compte la singularitat i la senzillesa del mètode japonès de comptar "Soroban". El mètode "Soroban" permet entrenar nens de 4 a 11 anys desenvolupant les seves capacitats mentals i ampliant el ventall de capacitats intel·lectuals dels nens.És fàcil ensenyar a qualsevol alumne a prendre exemples de matemàtiques a la ment utilitzant el mètode japonès de comptabilitat de sorobà. Practicant el recompte verbal mental, fem funcionar tot el cervell., descarregant així l’hemisferi esquerre, que és responsable de resoldre problemes matemàtics.
L'aritmètica mental permet fins i tot a l’hemisferi “figuratiu” interessar-se per les operacions computacionals, la qual cosa augmenta l’eficiència del cervell.
Un gran nombre requereix mètodes de càlcul escrits, tot i que hi ha individus que perfeccionen les seves habilitats per treballar amb ells.
Llegir exemples de matemàtiques a la ment és una necessitat vital, ja que els exàmens a l'escola ara no utilitzen calculadores, i la capacitat de comptar en la ment s'inclou en la llista de competències obligatòries dels graduats de 9 i 11 graus.
La regla bàsica per a l’addició mental és:
- Si el primer terme és un nombre de dos dígits (no una dotzena de rodes), afegiu-hi el següent 9: afegiu 10, elimineu 1.
- Afegiu 8: afegiu 10, elimineu 2.
Afegiu ràpidament números de dos dígits:
- Si l’últim dígit del segon terme és superior a 5, arrodoneu-lo. Realitzeu l’addició, elimineu l’additiu de l’import rebut.
- Si l’últim dígit del segon terme és inferior a 5, s’afegeix un dígit: primer, afegiu dotzenes i, a continuació, unitats.
- Podeu canviar els termes en llocs, però afegiu els números amb el mateix algorisme.
Característiques de la resta: reducció a números rodons
La deducció inequívoca s'arrodoneix fins a 10, de dos dígits, fins a 100. Resteu 10 o 100 i afegiu l’esmena. La recepció és rellevant per a petites esmenes.
Restar en compte els números de tres dígits
Basant-se en un bon coneixement de la composició dels números dels deu, podeu restar en parts en aquest ordre: centenars, desenes, unitats.
Podeu multiplicar-vos i dividir-vos sense problemes, coneixent la taula de multiplicar - "vareta màgica" per dominar ràpidament el compte en la vostra ment. Cal destacar que els nens del poble de Rússia pre-revolucionària van conèixer la continuació de l'anomenada taula pitagòrica (de l'11 al 19), i seria bo que els estudiosos moderns conegissin la taula fins al 19 * 9 de memòria.
Els trucs més interessants
Per captivar els nens amb les matemàtiques i fer que els moments difícils del currículum escolar siguin més propers i accessibles, hi ha maneres i mètodes, Convertir les dificultats en divertides i interessants:
- Per multiplicar un dígit de cada 9, mostrem a tots els nostres palmells buits. Doble el dit, corresponent en ordre (des del polze de la mà esquerra) fins al nombre del primer factor. Vam veure quants dits a l'esquerra de la inclinació: seran desenes de treballs desitjats i, a la dreta, la seva pròpia unitat.
- La multiplicació per 11 de qualsevol nombre de dos dígits, la suma dels quals no arriba a 10, és divertida i senzilla: moveu els dígits d’aquest número i poseu la seva suma entre ells: la resposta està preparada.
- Si la suma dels dígits multiplicada per 11 resulta ser 10 o més de 10, llavors entre els dígits de la quantitat mental separada hauríeu de posar la seva suma i afegir els dos primers dígits a l'esquerra, deixant els altres dos sense canvis, per obtenir el producte.
Per obtenir informació sobre com ensenyar a un nen a comptar instantàniament amb la vostra ment, vegeu el següent vídeo.