Πώς να μάθετε ένα παιδί να μετράει γρήγορα στο μυαλό σας;
Οι γονείς των σύγχρονων παιδιών με το φθόνο παρακολουθούν τους "geeks" - συμμετέχοντες στην τηλεοπτική εκπομπή "Best of All" και "Amazing People" - και ανησυχούν ότι τα παιδιά τους δεν διακρίνονται για την εξαιρετική τους νοημοσύνη και υπερηφάνεια: μαθηματικά.
Από την πρώτη τάξη βασίζονται σε δάκτυλα και ραβδιά, δεν γνωρίζουν τεχνικές προφορικής καταμέτρησης, επομένως έχουν μεγάλα προβλήματα σε όλα τα μαθήματα του σχολείου.
Οι τεχνικές της γρήγορης μέτρησης του στόματος είναι απλές και εύπεπτες, αλλά πρέπει να θυμόμαστε ότι η επιτυχημένη κυριαρχία τους δεν συνεπάγεται μηχανική, αλλά συνειδητή χρήση τεχνικών και, επιπλέον, περισσότερο ή λιγότερο μακρόχρονη εκπαίδευση.
Έχοντας καταλάβει τις στοιχειώδεις μεθόδους προφορικής απολογισμού, η χρήση τους θα είναι σε θέση να κάνει σωστά και γρήγορα τους άμεσους υπολογισμούς στο μυαλό με την ίδια ακρίβεια με τους γραπτούς υπολογισμούς.
Ειδικά χαρακτηριστικά
Υπάρχουν τόσες πολλές τεχνικές που προωθούν τη μάθηση για την επιτάχυνση της νοητικής αριθμητικής. Με όλες τις ορατές διαφορές, έχουν μια σημαντική ομοιότητα - βασίζονται σε τρεις «φάλαινες»:
- Εκπαίδευση και συσσώρευση εμπειρίας. Η τακτική πρακτική, η λύση των καθηκόντων από απλό σε σύνθετο, ποιοτικά και ποσοτικά, αλλάζει την ικανότητα των προφορικών υπολογισμών.
- Αλγόριθμος. Η γνώση και η εφαρμογή των "μυστικών" μεθόδων και νόμων απλοποιεί σε μεγάλο βαθμό τη διαδικασία της καταμέτρησης.
- Δυνατότητες και φυσικά οφέλη. Αναπτύχθηκε βραχυπρόθεσμη μνήμη και ο σημαντικός όγκος της, καθώς και η υψηλή συγκέντρωση της προσοχής - μια μεγάλη βοήθεια στην άσκηση μιας γρήγορης νοητικής αριθμητικής. Ένα συγκεκριμένο πλεονέκτημα είναι η παρουσία μιας μαθηματικής νοοτροπίας και μιας προδιάθεσης στη λογική σκέψη.
Η χρήση του προφορικού λογαριασμού
Οι άνθρωποι δεν είναι ρομπότ σιδήρου, αλλά το γεγονός ότι δημιουργούν έξυπνες μηχανές μιλά για την πνευματική υπεροχή τους. Ένα άτομο πρέπει να διατηρεί συνεχώς τον εγκέφαλο του σε καλή κατάσταση, η οποία προωθείται ενεργά από την κατάρτιση δεξιοτήτων στην ψυχική αριθμητική.
Για την καθημερινή ζωή:
- ένας επιτυχημένος προφορικός λογαριασμός είναι ένας δείκτης μιας αναλυτικής νοοτροπίας.
- η κανονική νοητική αριθμητική θα σας σώσει από την πρώιμη άνοια και τον γεροντικό μαρασμό.
- η ικανότητά σας να προσθέσετε και να αφαιρέσετε καλά δεν θα σας επιτρέψει να εξαπατήσετε στο κατάστημα.
Για επιτυχή μελέτη:
- ενεργοποιείται η πνευματική δραστηριότητα.
- ανάπτυξη μνήμης, η ομιλία, η προσοχή, η ικανότητα να αντιλαμβάνονται τι ειπώθηκε κατά την ακρόαση, η ταχύτητα αντίδρασης, η εφευρετικότητα, η ικανότητα να βρούμε τους πιο ορθολογικούς τρόπους επίλυσης του προβλήματος.
- ενίσχυση της εμπιστοσύνης στις δυνατότητές τους.
Πότε πρέπει να ξεκινήσω τις σπουδές μου;
Σύμφωνα με μαθαίνοντας μυαλά (ψυχολόγοι και εκπαιδευτικοί), ένα παιδί από το τέταρτο έτος είναι ήδη σε θέση να προσθέσει και να αφαιρέσει. Μέχρι την ηλικία των 5 ετών, το ψίχουλο μπορεί ελεύθερα να λύσει παραδείγματα και απλά καθήκοντα. Αλλά αυτά είναι τα στατιστικά στοιχεία και τα παιδιά δεν προσαρμόζονται πάντοτε σε αυτό. Επομένως Όλα εδώ είναι καθαρά ατομικά.
Σε κάθε περίπτωση, η διδασκαλία των παιδιών να μετράει γρήγορα το κεφάλι τους καλύτερα πριν από την είσοδό τους στο σχολείο - θα υπάρξουν λιγότερα προβλήματα και μια προσφορά χρήσιμων δεξιοτήτων θα βοηθήσει στην επιτυχία των σύγχρονων σχολικών προγραμμάτων.
Κανόνες
Η βασίλισσα των Επιστημών - Μαθηματικών - έλαβε τη φροντίδα των μαθητών και έφτιαξε ένα σύνολο νόμων, αλγορίθμους και κανόνες, έχοντας το κατακτηθεί και με την επιδέξια χρήση τους, τα παιδιά θα αγαπήσουν μαθηματικά και ψυχική εργασία:
- Η ιδιότητα μεταφοράς της προσθήκης: Αντικατάσταση των στοιχείων της ενέργειας, έχουμε το ίδιο αποτέλεσμα.
- Η συνδυασμένη ιδιότητα προσθήκης: όταν προστίθενται τρεις ή περισσότεροι αριθμοί, οι δύο (ή περισσότερες) αριθμητικές τιμές μπορούν να αντικατασταθούν από το άθροισμά τους.
- Προσθήκη και αφαίρεση με τη μετάβαση από μια δωδεκάδα: προσθέστε ένα μεγαλύτερο στοιχείο
- Σε δεκάδες γύρους, και στη συνέχεια προσθέστε το υπόλοιπο του άλλου στοιχείου.
- Αρχικά αφαιρούμε τις μεμονωμένες μονάδες από τον αριθμό στο σημείο της δράσης και στη συνέχεια από τις δεκάδες γύρους αφαιρούμε το υπόλοιπο της έκπτωσης.
- Έχοντας παρουσιάσει το μειωμένο με τη μορφή του αθροίσματος δεκάδων και μονάδων, αφαιρούμε από τις δεκάδες των μεγαλύτερων μικρότερων και προσθέτουμε στην απάντηση τις μονάδες της μείωσης.
- Κατά την προσθήκη και αφαίρεση δεκάδων γύρων (που ονομάζονται ακόμα "στρογγυλοί" αριθμοί), δεκάδες μπορούν να θεωρηθούν ως μονάδες.
- Προσθήκη και αφαίρεση δεκάδων και μονάδων. Δεκάδες πιο βολικό να προσθέσετε στις δεκάδες, και μονάδες - σε μονάδες.
Προσθέτοντας έναν αριθμό στο άθροισμα
Οι μέθοδοι είναι οι εξής:
- Υπολογίζουμε την αξία του και στη συνέχεια προσθέτουμε αυτήν την τιμή σε αυτό.
- Το προσθέτουμε στον πρώτο όρο και στη συνέχεια προσθέτουμε το δεύτερο όρο στο αποτέλεσμα.
- Προσθέτουμε τον αριθμό στον δεύτερο όρο και στη συνέχεια προσθέτουμε τον πρώτο όρο στην απάντηση.
Η προσθήκη του ποσού στον αριθμό
Οι μέθοδοι είναι οι εξής:
- Υπολογίζουμε τη μαρτυρία του και στη συνέχεια προσθέτουμε τον αριθμό.
- Προσθέτουμε τον πρώτο όρο στον αριθμό και στη συνέχεια προσθέτουμε το δεύτερο όρο στο αποτέλεσμα.
- Προσθέτουμε τον δεύτερο όρο στον αριθμό και στη συνέχεια προσθέτουμε τον πρώτο όρο στο αποτέλεσμα.
Η προσθήκη δύο ποσών. Προσθέτοντας δύο ποσά, επιλέγουμε τον πιο βολικό τρόπο υπολογισμού.
Χρησιμοποιώντας τις κύριες ιδιότητες πολλαπλασιασμού
Οι τεχνικές έχουν ως εξής:
- Η ιδιότητα μεταφοράς του πολλαπλασιασμού. Αν αλλάξουμε τους παράγοντες σε μέρη, το προϊόν τους δεν θα αλλάξει.
- Η συνδυασμένη ιδιότητα του πολλαπλασιασμού. Όταν πολλαπλασιάζονται τρεις ή περισσότεροι αριθμοί, δύο (ή περισσότεροι) αριθμοί μπορούν να αντικατασταθούν από το προϊόν τους.
- Κατανομή ιδιοτήτων του πολλαπλασιασμού. Για να πολλαπλασιάσετε το άθροισμα με έναν αριθμό, είναι απαραίτητο να πολλαπλασιάσετε κάθε στοιχείο του με αυτόν τον αριθμό και να προσθέσετε τα προκύπτοντα έργα.
Πολλαπλασιάστε και διαιρέστε τους αριθμούς κατά 10 και 100
Τρόποι:
- Για να αυξήσετε οποιονδήποτε αριθμό κατά 10 φορές, πρέπει να προσθέσετε ένα μηδέν στα δεξιά.
- Για να γίνει αυτό 100 φορές, πρέπει να αντιστοιχιστούν δύο μηδενικά στα δεξιά.
- Για να μειώσετε τον αριθμό κατά 10 φορές, πρέπει να αποθέσετε ένα μηδέν προς τα δεξιά και να διαιρέσετε κατά 100 - δύο μηδενικά.
Πολλαπλασιάστε το ποσό με τον αριθμό
Τρόποι:
- 1η μέθοδος. Υπολογίστε το ποσό και πολλαπλασιάστε το με αυτήν την τιμή.
- 2ος τρόπος. Πολλαπλασιάστε τον αριθμό με κάθε addend και προσθέστε τις ληφθείσες απαντήσεις.
Πολλαπλασιάστε τον αριθμό με το άθροισμα
Τρόποι:
- 1η μέθοδος. Βρείτε το άθροισμα και πολλαπλασιάστε τον αριθμό αυτών που παίρνουμε.
- 2ος τρόπος. Πολλαπλασιάστε τον αριθμό με κάθε ένα από τα addends και προσθέστε τα έργα που προκύπτουν.
Διαχωρίζοντας το ποσό από τον αριθμό
Τρόποι:
- 1η μέθοδος. Υπολογίστε το ποσό και διαιρέστε τον με έναν αριθμό.
- 2ος τρόπος. Κάθε ένα από τα addends διαιρείται με τον αριθμό και τα προκύπτοντα δείγματα προστίθενται.
Διαίρεση του αριθμού του προϊόντος
Επιλογές:
- 1η μέθοδος. Διαχωρίστε τον αριθμό από τον πρώτο παράγοντα και, στη συνέχεια, διαιρέστε το αποτέλεσμα με τον δεύτερο παράγοντα.
- 2ος τρόπος. Διαχωρίστε τον αριθμό από τον δεύτερο παράγοντα και στη συνέχεια διαιρέστε το αποτέλεσμα με τον πρώτο παράγοντα.
Προβολές
Στα μαθήματα του προφορικού λόγου δίνεται ελάχιστος χρόνος, αλλά αυτό δεν υποβαθμίζει τη σημασία του για την ανάπτυξη της ψυχικής δραστηριότητας των παιδιών. Οι λεκτικές υπολογιστικές δεξιότητες σχηματίζονται στα μαθήματα των μαθηματικών στο δημοτικό σχολείο όταν εκτελούν διάφορους τύπους εργασιών και ασκήσεων.
Βρείτε την αξία μιας μαθηματικής έκφρασης
Αυτές μπορεί να είναι συνήθεις αριθμητικές εκφράσεις ή εκφράσεις με μεταβλητή (αλφαβητική) και οι αριθμητικές τιμές προτείνονται για γράμματα.Αντικαθιστώντας τους αριθμούς αντί των γραμμάτων, βρείτε την αριθμητική τιμή της έκφρασης που προκύπτει.
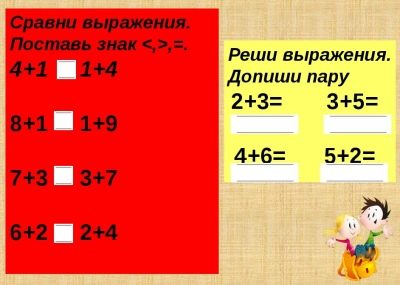
Συγκρίνετε εκφράσεις μαθηματικών
Τέτοιες εργασίες ποικίλλουν:
- να προσδιοριστεί η ισότητα ή η ανισότητα αυτών των δύο εκφράσεων (μετά την εύρεση και σύγκριση των αξιών τους).
- στη σχέση που δίνεται στο σημείο και μία από τις εκφράσεις για να συνθέσουμε τη δεύτερη έκφραση ή να ολοκληρώσουμε την ημιτελή προτεινόμενη
- σε τέτοιες ασκήσεις, μπορούν να χρησιμοποιηθούν μονοψήφιες, διψήφιες, τριψήφιες αριθμοί και ποσότητες στις εκφράσεις και στις τέσσερις αριθμητικές πράξεις. Ο κύριος σκοπός αυτών των καθηκόντων είναι μια σταθερή αφομοίωση του θεωρητικού υλικού και η ανάπτυξη υπολογιστικών δεξιοτήτων.
- Λύστε τις εξισώσεις. Βοηθούν στην κατανόηση των συνδέσεων μεταξύ των στοιχείων και των αποτελεσμάτων των αριθμητικών λειτουργιών.
- Λύστε το πρόβλημα. Μπορεί να είναι απλά και πολύπλοκα καθήκοντα. Με τη βοήθειά τους, ενισχύεται η θεωρητική γνώση, αναπτύσσονται υπολογιστικές δεξιότητες και δεξιότητες, ενεργοποιείται η πνευματική δραστηριότητα των παιδιών.
Δέσμες απόρριψης λογαριασμού
Σημεία διαίρεσης αριθμών:
- από 2: όλα αυτά υπερβαίνουν, και στην αριθμητική σειρά περνούν από ένα?
- στις 3 και 9: εάν το άθροισμα των ψηφίων είναι πολλαπλάσιο των δεικτών αυτών χωρίς ισορροπία.
- κατά 4: αν τα τελευταία δύο ψηφία του αρχείου σχηματίζουν διαδοχικά έναν αριθμό που διαιρείται με 4,
- 5: στρογγυλά δεκάδες και εκείνα όπου υπάρχουν 5 στο τέλος?
- από 6: οι αριθμοί που είναι πολλαπλάσιοι των δύο και οι τρεις διαιρούνται.
- 10: Αριθμητικές τιμές, στις οποίες το αρχείο είναι στο τέλος είναι 0.
- 12: διαιρέστε τους αριθμούς που μπορούν να χωριστούν σε τρία και τέσσερα ταυτόχρονα.
- κατά 15: αριθμοί που διαιρούνται ταυτόχρονα σε ενιαία συνιστώσα ενιαίας αξίας αυτού του αριθμού παραγόντων.
Φόρμα πρωτοβάθμιου σχολείου
Είναι γνωστό ότι η κύρια δραστηριότητα των προσχολικών και των νεότερων φοιτητών είναι ένα παιχνίδι που είναι χρήσιμο να συμπεριληφθεί σε όλα τα στάδια του μαθήματος. Ορισμένες μορφές του προφορικού λογαριασμού θα δοθούν παρακάτω.
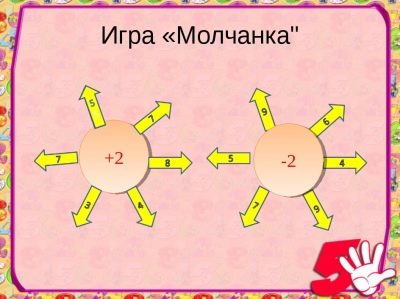
Το παιχνίδι "Silent"
Βοηθάει στην καλλιέργεια της προσοχής και της πειθαρχίας. Μια σιωπή μπορεί να αποτελείται από παραδείγματα σε μία ενέργεια, δύο ή περισσότερα. Παίζεται σε όλες τις τάξεις του δημοτικού σχολείου με αφηρημένους ακεραίους και ονομασμένους αριθμούς.
Οι μαθητές θεωρούν στο μυαλό τους και σιωπηλά την κλήση, οι καθηγητές γράφουν τις απαντήσεις στα παραδείγματα που τους προσφέρονται στον μαυροπίνακα. Οι σωστές απαντήσεις ικανοποιούνται με ελαφριά χτυπήματα και λάθος απαντήσεις με σιωπή.
Παιχνίδι "Lotto"
Μπορεί να υπάρχουν διάφοροι τύποι που αντιστοιχούν στα τμήματα των μαθηματικών που μελετώνται και πρέπει να καθοριστούν. Για παράδειγμα, lotto με παραδείγματα πολλαπλασιασμού και διαίρεσης μέσα στα "εκατοντάδες".
Για να δώσουμε μεγαλύτερο ενδιαφέρον στο παιχνίδι, ελαστικά με απαντήσεις μπορούν να γίνουν από μια κομμένη εικόνα. Εάν όλα τα παραδείγματα λυθούν σωστά, γίνεται μια εικόνα από τα ελαστικά.
Παιχνίδι "Αριθμητικοί λαβύρινθοι"
Μοιάζουν με ομόκεντρους κύκλους με πύλες με αριθμούς. Για να φτάσετε στο κέντρο, πρέπει να καλέσετε έναν αριθμό στο κέντρο. Οι λαβύρινθοι για την απόφαση μπορούν να απαιτήσουν είτε μία ενέργεια (προσθήκη) είτε πολλές. Πρέπει να σημειωθεί ότι αυτά τα καθήκοντα έχουν διάφορες λύσεις.
Το παιχνίδι "Πιάσε τον πιλότο" (ένα είδος "σκάλας")
Στο σχέδιο πίνακα: ένα αεροπλάνο με βρόχους, στα οποία παραδείγματα. Δύο κατηγόρητοι μαθητές καταγράφουν τις απαντήσεις στα αριστερά και στα δεξιά των βρόχων. Ποιος αποφασίζει σωστά και γρήγορα, θα προλάβει τον πιλότο.
Το παιχνίδι "Κυκλικά Παραδείγματα"
Το διδακτικό υλικό είναι ένα σύνολο καρτών, διατεταγμένων σε φακέλους. Κάθε ένα από αυτά έχει 8 κάρτες, καθένα από τα οποία περιέχει ένα παράδειγμα.
Τα αριθμητικά παραδείγματα σε κάθε φάκελο διαφέρουν ως προς το περιεχόμενό τους και επιλέγονται σύμφωνα με την αρχή του αυτοέλεγχου: στην επίλυσή τους, το αποτέλεσμα ενός παραδείγματος θα είναι η αρχή του επόμενου.
Κυκλικά παραδείγματα μπορούν να προσφερθούν ως σκάλες.
Μέθοδοι και τεχνικές ανάπτυξης
Λαμβάνοντας υπόψη τους τρόπους διδασκαλίας των παιδιών των 6 ετών για γρήγορη καταμέτρηση στο μυαλό τους, είναι αδύνατο να μην σημειωθεί η μοναδικότητα και η απλότητα της ιαπωνικής μεθόδου μέτρησης του «Soroban». Η τεχνική Soroban σας επιτρέπει να εκπαιδεύετε παιδιά ηλικίας 4 έως 11 ετών, αναπτύσσοντας τις ψυχικές τους ικανότητες και διευρύνοντας το φάσμα των πνευματικών ικανοτήτων των παιδιών.Είναι εύκολο να διδάξετε σε οποιονδήποτε μαθητή να λάβει παραδείγματα μαθηματικών στο μυαλό, χρησιμοποιώντας την ιαπωνική μέθοδο μέτρησης του σορβονανίου. Με την άσκηση πνευματικών λεκτικών μετρήσεων, βάζουμε σε λειτουργία ολόκληρο τον εγκέφαλο., εκφορτώντας έτσι το αριστερό ημισφαίριο, το οποίο είναι υπεύθυνο για την επίλυση μαθηματικών προβλημάτων.
Η νοητική αριθμητική επιτρέπει ακόμη και στο «εικονιστικό» ημισφαίριο να ενδιαφέρεται για υπολογιστικές λειτουργίες, γεγονός που αυξάνει την αποτελεσματικότητα του εγκεφάλου.
Μεγάλοι αριθμοί απαιτούν γραπτές μεθόδους υπολογισμού, αν και υπάρχουν άτομα που ακονίζουν τις δεξιότητές τους για να συνεργαστούν μαζί τους.
Λαμβάνοντας υπόψη τα παραδείγματα των μαθηματικών στο μυαλό είναι μια ζωτική ανάγκη, δεδομένου ότι οι εξετάσεις στο σχολείο είναι τώρα χωρίς τη χρήση αριθμομηχανών και η ικανότητα να μετράνε το μυαλό περιλαμβάνεται στον κατάλογο των υποχρεωτικών δεξιοτήτων των πτυχιούχων βαθμών 9 και 11.
Ο βασικός κανόνας για τη διανοητική προσθήκη είναι:
- Αν ο πρώτος όρος είναι ένας διψήφιος αριθμός (όχι μια στρογγυλή δωδεκάδα), προσθέστε 9 σε αυτόν ως εξής: προσθέστε 10, αφαιρέστε 1.
- Προσθήκη 8: προσθήκη 10, κατάργηση 2.
Προσθέστε γρήγορα διψήφια αριθμούς:
- Αν το τελευταίο ψηφίο του δεύτερου όρου είναι μεγαλύτερο από 5, στρέψτε το προς τα πάνω. Εκτελούμε την προσθήκη, από το προκύπτον ποσό αφαιρούμε το "πρόσθετο".
- Εάν το τελευταίο ψηφίο του δεύτερου όρου είναι μικρότερο από 5, τότε προσθέστε τα ψηφία: πρώτα, προσθέστε δεκάδες, έπειτα - μονάδες.
- Μπορείτε να αλλάξετε τους όρους σε μέρη, αλλά να προσθέσετε τους αριθμούς χρησιμοποιώντας τον ίδιο αλγόριθμο.
Χαρακτηριστικά αφαίρεσης: μείωση σε αριθμούς γύρων
Η αδιαμφισβήτητη έκπτωση είναι στρογγυλοποιημένη έως 10, δύο ψηφία - έως 100. Αφαιρέστε 10 ή 100 και προσθέστε την τροπολογία. Η υποδοχή αφορά μικρές τροποποιήσεις.
Αφαιρέστε τους τριψήφιους αριθμούς
Με βάση την καλή γνώση της σύνθεσης των αριθμών των πρώτων δέκα, μπορείτε να αφαιρέσετε σε μέρη με αυτή τη σειρά: εκατοντάδες, δεκάδες, μονάδες.
Ο πολλαπλασιασμός και ο διαχωρισμός μπορεί να είναι εύκολα, γνωρίζοντας τον πίνακα πολλαπλασιασμού - "μαγικό ραβδί" στην ταχεία ανάπτυξη του λογαριασμού στο μυαλό. Αξίζει να σημειωθεί ότι τα παιδιά του χωριού της προ-επαναστατικής Ρωσίας γνώριζαν τη συνέχιση του λεγόμενου Πυθαγορείου πίνακα - από τις 11 έως τις 19 και θα ήταν ωραίο για τους σύγχρονους μελετητές να γνωρίζουν το τραπέζι μέχρι το 19 * 9.
Τα πιο ενδιαφέροντα κόλπα
Για να αιχμαλωτίσουν τα παιδιά με τα μαθηματικά και να κάνουν τις δύσκολες στιγμές στο σχολικό πρόγραμμα πιο κοντά και πιο προσιτές, υπάρχουν τρόποι και μέθοδοι, Η μετατροπή των δυσκολιών σε διασκέδαση και ενδιαφέρον:
- Για να πολλαπλασιάσετε οποιοδήποτε μονοψήφιο αριθμό κατά 9, ας δείξουμε σε όλους τους άδειους φοίνικες. Κατεβάστε το δάκτυλό σας, που αντιστοιχεί στη σειρά (μετρώντας από τον αντίχειρα του αριστερού χεριού) στον αριθμό του πρώτου παράγοντα. Εξετάζουμε πόσα δάχτυλα στα αριστερά του λυγισμένα - θα είναι δεκάδες από το επιθυμητό έργο, και δεξιά - η δική του μονάδα.
- Ο πολλαπλασιασμός κατά 11 οποιωνδήποτε διψήφιων αριθμών, το άθροισμα των οποίων δεν φθάνει το 10, είναι διασκεδαστικό και απλό: μετακινήστε διανοητικά τα ψηφία αυτού του αριθμού και βάλτε το άθροισμά τους μεταξύ τους - η απάντηση είναι έτοιμη.
- Εάν το άθροισμα των ψηφίων πολλαπλασιασμένο επί 11 αποδειχθεί ότι είναι 10 ή μεγαλύτερο από 10, τότε μεταξύ των διανοητικά διατεταγμένων ψηφίων αυτού του αριθμού πρέπει να βάλετε το άθροισμά τους και να προσθέσετε τα δύο πρώτα ψηφία προς τα αριστερά, αφήνοντας τα άλλα δύο αμετάβλητα, για να πάρετε το προϊόν.
Για πληροφορίες σχετικά με τον τρόπο διδασκαλίας του παιδιού σας να μετράει άμεσα το μυαλό σας, δείτε το παρακάτω βίντεο.