¿Cómo aprender a un niño a contar rápidamente en tu mente?
Los padres de niños modernos con envidia miran a los geeks, participantes del programa de televisión "Best of All" y "Amazing People", y se preocupan de que sus hijos no se distingan por su inteligencia y su ingenio sobresalientes: aprenden mal el programa de la escuela primaria, no les gusta forzar el cerebro y temen las lecciones matematicas
Desde la primera clase cuentan con dedos y varitas, no conocen las técnicas de conteo oral, por lo que tienen grandes problemas en todas las materias del curso escolar.
Las técnicas de conteo oral rápido son simples y fáciles de digerir, pero debe recordarse que el dominio exitoso de ellas implica un uso no mecánico, pero bastante consciente de las técnicas y, además, un entrenamiento más o menos prolongado.
Una vez que domine los métodos elementales de la cuenta oral, al usarlos podrá realizar cálculos instantáneos en la mente de manera correcta y rápida con la misma precisión que con los cálculos escritos.
Características especiales
Hay muchas técnicas que promueven el aprendizaje rápido del conteo mental. Con todas las diferencias visibles, tienen una similitud importante: se basan en tres "ballenas":
- Formación y acumulación de experiencias. La práctica regular, la solución de tareas de simple a compleja, cambia cualitativamente y cuantitativamente la habilidad de la computación oral.
- Algoritmo El conocimiento y la aplicación de métodos y leyes "secretas" simplifican enormemente el proceso de conteo.
- Habilidades y dotaciones naturales. Desarrolló la memoria a corto plazo y su considerable volumen, así como una alta concentración de atención, una gran ayuda para practicar una aritmética mental rápida. Una ventaja definitiva es la presencia de una mentalidad matemática y una predisposición al pensamiento lógico.
El uso de la cuenta oral.
Las personas no son robots de hierro, pero el hecho de que creen máquinas inteligentes habla de su superioridad intelectual. Una persona necesita mantener constantemente su cerebro en buena forma, lo cual es promovido activamente por el entrenamiento de habilidades en aritmética mental.
Para la vida cotidiana:
- una cuenta oral exitosa es un indicador de una mentalidad analítica;
- La aritmética mental regular lo salvará de la demencia temprana y el marasmo senil;
- tu habilidad para sumar y restar bien no te permitirá hacer trampa en la tienda.
Para un estudio exitoso:
- se activa la actividad mental;
- desarrollar la memoriadiscurso, atención, capacidad para percibir lo que se dijo en la audiencia, velocidad de reacción, ingenio, capacidad para encontrar las formas más racionales de resolver el problema;
- Fortalecimiento de la confianza en sus capacidades.
¿Cuándo debo empezar mis estudios?
Según las mentes aprendidas (psicólogos y educadores), un niño para el cuarto año ya puede sumar y restar. A la edad de 5 años, la miga puede resolver libremente ejemplos y tareas simples. Pero esto es estadística, y los niños no siempre se adaptan a ella. Por lo tanto Todo aquí es puramente individual.
En cualquier caso, es mejor enseñarles a los niños a contar mentalmente rápidamente antes de ingresar a la escuela; habrá menos problemas y una cantidad de habilidades útiles ayudará a dominar los programas escolares modernos con más éxito.
Las reglas
La Reina de las Ciencias - Matemáticas - se hizo cargo de los estudiantes e hizo un conjunto de leyes, Los algoritmos y las reglas, al dominarlos y usarlos hábilmente, a los niños les encantarán las matemáticas y el trabajo mental:
- La propiedad de transferencia de la adición: intercambiando los componentes de la acción, obtenemos el mismo resultado.
- La propiedad de adición combinada: cuando se suman tres o más números, cualquier dos (o más) valores numéricos se pueden reemplazar por su suma.
- Suma y resta con la transición a través de una docena: agrega un componente más grande
- Para docenas de redondeos, y luego agregue el resto del otro componente.
- Reste primero las unidades individuales del número al signo de la acción, y luego de las docenas de rondas restamos el resto del deducible.
- Habiendo presentado la disminución en la forma de la suma de decenas y unidades, eliminamos de las decenas de las más grandes a las más pequeñas y agregamos a la respuesta las unidades de la disminución.
- Al sumar y restar docenas de rondas (aún se llaman números "redondos"), docenas pueden considerarse lo mismo que unidades.
- Suma y resta de decenas y unidades. Docenas más convenientes de agregar a las decenas y unidades a las unidades.
Sumando un número a la suma
Los métodos son los siguientes:
- Calculamos su valor y luego le agregamos este valor.
- Lo agregamos al primer término y luego agregamos el segundo término al resultado.
- Agregamos el número al segundo término y luego agregamos el primer término a la respuesta.
La suma del importe al número.
Los métodos son los siguientes:
- Calculamos su testimonio, y luego lo sumamos al número.
- Agregamos el primer término al número, y luego agregamos el segundo término al resultado.
- Agregamos el segundo término al número, y luego agregamos el primer término al resultado.
La suma de dos sumas. Sumando dos sumas, elegimos la forma más conveniente de calcular.
Usando las principales propiedades de multiplicación.
Las técnicas son las siguientes:
- La propiedad de transferencia de la multiplicación. Si cambiamos los factores en lugares, su producto no cambiará.
- La propiedad combinada de la multiplicación. Al multiplicar tres o más números, cualquier dos (o más) números pueden ser reemplazados por su producto.
- Distribución de la propiedad de la multiplicación. Para multiplicar la suma por un número, es necesario multiplicar cada uno de sus componentes por este número y agregar los trabajos resultantes.
Multiplica y divide números por 10 y 100.
Maneras:
- Para aumentar cualquier número por 10 veces, debe agregar un cero a la derecha.
- Para hacer esto 100 veces, deben asignarse dos ceros a la derecha.
- Para reducir el número en 10 veces, debe colocar un cero a la derecha y dividir por 100 - dos ceros.
Multiplica la cantidad por el número.
Maneras:
- 1er método. Calcula la cantidad y multiplícala por este valor.
- 2ª vía. Multiplique el número con cada uno de los sumandos y agregue las respuestas recibidas.
Multiplicar numero por suma
Maneras:
- 1er método. Encuentra la suma y multiplica el número de lo que obtenemos.
- 2ª vía. Multiplique el número por cada uno de los sumandos y agregue los trabajos resultantes.
Dividiendo la cantidad por el número
Maneras:
- 1er método. Calcula la cantidad y divídelo por un número.
- 2ª vía. Cada uno de los sumandos se divide por el número y se agregan los cocientes resultantes.
Dividiendo el número del producto.
Opciones:
- 1er método. Divida el número por el primer factor y luego divida el resultado por el segundo factor.
- 2ª vía. Divida el número por el segundo factor, y luego divida el resultado por el primer factor.
Vistas
En las lecciones sobre la cuenta oral se da poco tiempo, pero esto no le resta importancia al desarrollo de la actividad mental de los niños. Las habilidades computacionales verbales se forman en las lecciones de matemáticas en la escuela primaria cuando se realizan varios tipos de tareas y ejercicios.
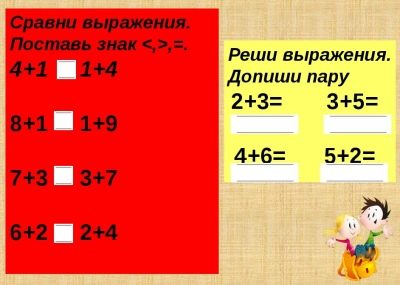
Encuentra el valor de una expresión matemática
Estas pueden ser expresiones numéricas ordinarias o expresiones con una variable (alfabética), y se sugieren valores numéricos para las letras.Sustituyendo números en lugar de letras, encuentre el valor numérico de la expresión resultante.
Compara expresiones de matematicas
Tales tareas son variadas:
- determinar la igualdad o desigualdad de estas dos expresiones (después de encontrar y comparar sus valores);
- a la relación dada al signo y una de las expresiones para componer la segunda expresión o para completar la propuesta inacabada;
- en dichos ejercicios, se pueden usar números y cantidades de un dígito, de dos dígitos, de tres dígitos en las expresiones y en las cuatro operaciones aritméticas. El propósito principal de tales tareas es una sólida asimilación del material teórico y el desarrollo de habilidades computacionales.
- Resuelve las ecuaciones. Ayudan a comprender las conexiones entre los componentes y los resultados de las operaciones aritméticas.
- Resuelve el problema. Puede ser tanto tareas simples como complejas. Con su ayuda, se fortalecen los conocimientos teóricos, se desarrollan habilidades computacionales y se activa la actividad mental de los niños.
Cuentas orales de recepciones.
Señales de divisibilidad de números:
- por 2: todos los que lo superan, y en la fila numérica pasan por uno;
- en 3 y 9: si la suma de los dígitos es un múltiplo de estos indicadores sin saldo;
- por 4: si los dos últimos dígitos del registro forman sucesivamente un número que está dividido por 4;
- 5: docenas redondas y aquellas donde hay 5 al final;
- por 6: los números que son múltiplos de dos y tres están divididos;
- 10: valores numéricos, en los que el registro está al final es 0;
- 12: divide los números que se pueden dividir en tres y cuatro al mismo tiempo;
- por 15: números que se dividen al mismo tiempo en componentes integrales de un solo valor de estos factores numéricos.
Formularios de cuenta de la escuela primaria
Es bien sabido que la actividad principal de los niños en edad preescolar y los más pequeños es un juego que es útil para incluir en todas las etapas de la lección. Algunas formas de la cuenta oral se darán a continuación.
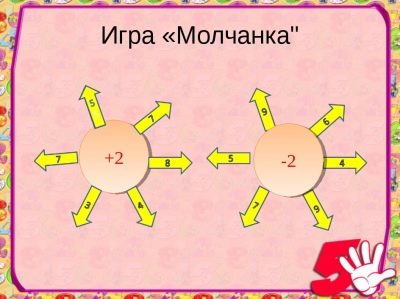
El juego "silencioso"
Ayuda a cultivar la atención y la disciplina. Un silencio puede consistir en ejemplos en una acción, dos o más. Se juega en todas las clases de la escuela primaria con enteros abstractos y números con nombre.
Los estudiantes consideran en sus mentes y en silencio en la llamada, los maestros escriben las respuestas a los ejemplos que se les ofrecen en la pizarra. Las respuestas correctas se encuentran con aplausos ligeros, y las respuestas incorrectas con silencio.
Juego "Lotto"
Puede haber varios tipos correspondientes a las secciones de matemáticas que se estudian y necesitan ser arregladas. Por ejemplo, lotería con ejemplos de multiplicación y división dentro de los "cientos".
Para darle más interés al juego, se pueden hacer llantas con respuestas a partir de una imagen cortada. Si todos los ejemplos se resuelven correctamente, se hace una imagen de los neumáticos.
Juego "Laberintos aritméticos"
Se ven como círculos concéntricos con puertas con números. Para llegar al centro, debe marcar un número en el centro. Los laberintos para la decisión pueden exigir una acción (adición) o varias. Cabe señalar que estas tareas tienen varias soluciones.
El juego "Atrapa al piloto" (una especie de "escalera")
En el tablero de dibujo: un plano con bucles, en el que aparecen ejemplos. Dos estudiantes convocados registran las respuestas a la izquierda y derecha de los bucles. Quien decide correcta y rápidamente, se pondrá al día con el piloto.
El juego "Ejemplos circulares"
El material didáctico es un conjunto de tarjetas, dispuestas en sobres; Cada una de ellas tiene 8 cartas, cada una de las cuales contiene un ejemplo.
Los ejemplos numéricos en cada sobre son diferentes en su contenido y se seleccionan de acuerdo con el principio de autocontrol: al resolverlos, el resultado de un ejemplo será el comienzo del siguiente.
Ejemplos circulares pueden ser ofrecidos como escaleras.
Métodos y técnicas de desarrollo.
Teniendo en cuenta las formas de enseñar a los niños de 6 años a contar rápidamente en su mente, es imposible no notar la singularidad y simplicidad del método japonés de contar "Soroban". La técnica de Soroban le permite entrenar a niños de 4 a 11 años, desarrollando sus capacidades mentales y ampliando la gama de habilidades intelectuales de los niños.Es fácil enseñar a cualquier estudiante a tomar ejemplos de matemáticas en la mente, usando el método japonés de contar con sorobane. Al practicar los conteos verbales mentales, ponemos en funcionamiento todo el cerebro., descargando así el hemisferio izquierdo, que es responsable de resolver problemas matemáticos.
La aritmética mental permite que incluso el hemisferio "figurativo" se interese en operaciones computacionales, lo que aumenta la eficiencia del cerebro.
Los números grandes requieren métodos de cálculo escritos, aunque hay personas que perfeccionan sus habilidades para trabajar con ellos.
Teniendo en cuenta ejemplos de matemáticas en la mente es una necesidad vital, ya que los exámenes en la escuela ahora están sin el uso de calculadoras, y la capacidad de contar mentalmente se incluye en la lista de habilidades obligatorias de los graduados de 9 y 11 grados.
La regla básica para la adición mental es:
- Si el primer término es un número de dos dígitos (no una docena redonda), luego agregue 9 de la siguiente manera: agregue 10, elimine 1.
- Añadir 8: agregar 10, eliminar 2.
Agregue rápidamente números de dos dígitos:
- Si el último dígito del segundo término es mayor que 5, redondéelo hacia arriba. Realizamos la adición, de la cantidad resultante eliminamos el "aditivo".
- Si el último dígito del segundo término es menor que 5, luego sume por dígitos: primero, agregue docenas, luego - unidades.
- Puede intercambiar los términos en lugares, pero agregue los números usando el mismo algoritmo.
Características de la resta: reducción a números redondos
El deducible no ambiguo se redondea a 10, dos dígitos, hasta 100. Reste 10 o 100 y agregue la enmienda. La recepción es relevante para pequeñas enmiendas.
Resta números de tres dígitos en mente
Sobre la base de un buen conocimiento de la composición de los números de los diez, puede restar en partes en este orden: cientos, decenas, unidades.
Multiplicar y dividir puede ser fácil, conociendo la tabla de multiplicar - "varita mágica" para el rápido desarrollo de la cuenta en la mente. Cabe destacar que los niños de la aldea de la Rusia pre-revolucionaria conocieron la continuación de la llamada mesa de Pitágoras, del 11 al 19, y sería bueno para los estudiosos modernos conocer la mesa hasta las 19 * 9 de memoria.
Los trucos mas interesantes.
Para cautivar a los niños con las matemáticas y hacer que los momentos difíciles en el currículo escolar sean más cercanos y más accesibles, hay formas y métodos, Convirtiendo las dificultades en divertidas e interesantes:
- Para multiplicar cualquier dígito por 9, mostremos a todos nuestras palmas vacías. Doble su dedo, correspondiendo en orden (contando desde el pulgar de la mano izquierda) hasta el número del primer factor. Miramos cuántos dedos a la izquierda de la curva - serán docenas del trabajo deseado, y a la derecha - su propia unidad.
- La multiplicación por 11 de cualquier número de dos dígitos, cuya suma no llega a 10, es divertida y simple: mueva mentalmente los dígitos de este número y ponga su suma entre ellos; la respuesta está lista.
- Si la suma de dígitos multiplicada por 11 resulta ser 10 o más de 10, entonces, entre los dígitos espaciados mentalmente de este número, debe colocar su suma y agregar los primeros dos dígitos a la izquierda, dejando los otros dos sin cambios, para obtener el producto.
Para obtener información sobre cómo enseñarle a su hijo a contar instantáneamente en su mente, vea el siguiente video.