Comment apprendre à un enfant à compter rapidement dans votre esprit?
Des parents d’enfants modernes et envieux regardent les geeks - participants à l’émission télévisée "Best of All" et "Amazing People" - et s’inquiètent de ce que leurs enfants ne se distinguent pas par leur intelligence et leur super esprit: ils apprennent mal le programme de l’école élémentaire, ils n’aiment pas se fatiguer la cervelle et ont peur des leçons les mathématiques.
Dès le premier cours, ils comptent sur les doigts et les baguettes, ils ne connaissent pas les techniques de dénombrement oral, ils ont donc de gros problèmes dans toutes les matières du cours.
Les techniques de comptage oral rapide sont simples et faciles à digérer, mais il faut se rappeler que leur maîtrise réussie implique une utilisation non mécanique, mais tout à fait conscient des techniques et, en outre, une formation plus ou moins longue.
Après avoir maîtrisé les méthodes élémentaires de récit oral, leur utilisation permettra d'effectuer correctement et rapidement des calculs instantanés dans l'esprit avec la même précision que les calculs écrits.
Caractéristiques spéciales
Il y a tellement de techniques qui favorisent l'apprentissage pour accélérer le calcul mental. Avec toutes les différences visibles, elles ont une similitude importante - elles sont basées sur trois "baleines":
- Formation et accumulation d'expérience. La pratique régulière, la résolution de tâches simples à complexes, qualitativement et quantitativement, modifie les compétences du calcul oral.
- Algorithme. La connaissance et l'application de méthodes et de lois «secrètes» simplifient grandement le processus de comptage.
- Capacités et dotations naturelles. La mémoire à court terme développée et son volume considérable, ainsi que la concentration de l’attention - une grande aide dans la pratique d’une arithmétique mentale rapide. Un avantage certain est la présence d'un état d'esprit mathématique et une prédisposition à la pensée logique.
L'utilisation du compte oral
Les gens ne sont pas des robots ferreux, mais le fait qu'ils créent des machines intelligentes témoigne de leur supériorité intellectuelle. Une personne doit constamment garder son cerveau en forme, ce qui est activement encouragé par l’acquisition de compétences en calcul mental.
Pour la vie quotidienne:
- un compte rendu oral réussi est un indicateur d'un état d'esprit analytique;
- Une arithmétique mentale régulière vous évitera la démence précoce et le marasme sénile;
- votre capacité à bien additionner et soustraire ne vous permettra pas de tricher dans le magasin.
Pour une étude réussie:
- l'activité mentale est activée;
- développer la mémoire, parole, attention, capacité à percevoir ce qui a été dit à l'audience, rapidité de réaction, ingéniosité, capacité à trouver les moyens les plus rationnels de résoudre le problème;
- confiance accrue dans leurs capacités.
Quand devrais-je commencer mes études?
Selon les esprits instruits (psychologues et éducateurs), un enfant de 4 ans est déjà en mesure de faire des additions et des soustractions. À l'âge de 5 ans, la miette peut résoudre librement des exemples et des tâches simples. Mais ce sont des statistiques et les enfants ne s’y adaptent pas toujours. Donc Tout ici est purement individuel.
Quoi qu’il en soit, il est préférable d’apprendre aux enfants à compter rapidement dans leur tête avant d’aller à l’école - les problèmes seront moins nombreux et un ensemble de compétences utiles aidera à mieux maîtriser les programmes scolaires modernes.
Les règles
La reine des sciences - Mathématiques - s’occupait des élèves et faisait un ensemble de lois, Algorithmes et règles, maîtrisés et maîtrisés, les enfants vont adorer les mathématiques et le travail mental:
- La propriété de transfert de l'addition: en échangeant les composants de l'action, on obtient le même résultat.
- La propriété d'addition combinée: lorsque trois ou plusieurs nombres sont additionnés, deux valeurs numériques (ou plus) peuvent être remplacées par leur somme.
- Addition et soustraction avec la transition sur une douzaine: ajouter un composant plus grand
- Pour des dizaines de tours, puis ajoutez le reste de l'autre composant.
- Soustrayez d’abord les unités individuelles du nombre au signe de l’action, puis des dizaines de tours, soustrayez le reste de la franchise.
- Après avoir présenté le diminué sous la forme de la somme des dizaines et des unités, nous retirons des dizaines des plus grands et des plus petits et ajoutons à la réponse les unités du diminuant.
- Lorsque vous ajoutez et soustrayez des dizaines de tours (on les appelle encore des nombres «ronds»), vous pouvez considérer des dizaines comme des unités.
- Addition et soustraction de dizaines et d'unités. Des dizaines plus pratiques à ajouter aux dizaines et aux unités - aux unités.
Ajouter un nombre à la somme
Les méthodes sont les suivantes:
- Nous calculons sa valeur, puis lui ajoutons cette valeur.
- Nous l'ajoutons au premier terme, puis nous ajoutons le deuxième terme au résultat.
- Nous ajoutons le nombre au deuxième terme, puis le premier terme à la réponse.
L'ajout du montant au nombre
Les méthodes sont les suivantes:
- Nous calculons son témoignage, puis nous ajoutons au nombre.
- Nous ajoutons le premier terme au nombre, puis le second terme au résultat.
- Nous ajoutons le second terme au nombre, puis le premier terme au résultat.
L'ajout de deux sommes. En ajoutant deux sommes, nous choisissons la méthode de calcul la plus pratique.
Utiliser les principales propriétés de multiplication
Les techniques sont les suivantes:
- La propriété de transfert de la multiplication. Si nous changeons les facteurs à certains endroits, leur produit ne changera pas.
- La propriété combinée de la multiplication. Lors de la multiplication de trois nombres ou plus, deux (ou plus) nombres peuvent être remplacés par leur produit.
- Propriété de distribution de la multiplication. Pour multiplier la somme par un nombre, il est nécessaire de multiplier chacune de ses composantes par ce nombre et d'ajouter les travaux résultants.
Multipliez et divisez les nombres par 10 et 100
Manières:
- Pour augmenter un nombre de 10 fois, vous devez ajouter un zéro à droite.
- Pour le faire 100 fois, il faut lui attribuer deux zéros à droite.
- Pour réduire le nombre de 10 fois, vous devez supprimer un zéro à droite et diviser par 100 - deux zéros.
Multipliez le montant par le nombre
Manières:
- 1ère méthode. Calculez le montant et multipliez-le par cette valeur.
- 2ème voie. Multipliez le nombre avec chacun des ajouts et ajoutez les réponses reçues.
Multiplier le nombre par la somme
Manières:
- 1ère méthode. Trouvez la somme et multipliez le nombre de ce que nous obtenons.
- 2ème voie. Multipliez le nombre par chacun des ajouts et ajoutez les travaux résultants.
Diviser le montant par le nombre
Manières:
- 1ère méthode. Calculez le montant et divisez-le par un nombre.
- 2ème voie. Chacun des additifs est divisé par le nombre et les quotients résultants sont ajoutés.
Division du numéro du produit
Options:
- 1ère méthode. Divisez le nombre par le premier facteur, puis le résultat par le deuxième facteur.
- 2ème voie. Divisez le nombre par le deuxième facteur, puis le résultat par le premier facteur.
Des vues
Au cours des leçons orales, on parle de peu de temps, mais cela n'enlève rien à son importance pour le développement de l'activité mentale des enfants. Des habiletés de calcul verbales sont formées lors des cours de mathématiques au primaire lors de l'exécution de divers types de tâches et d'exercices.
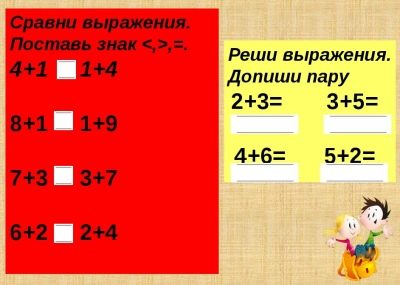
Trouver la valeur d'une expression mathématique
Il peut s'agir d'expressions numériques ordinaires ou d'expressions avec une variable (alphabétique). Des valeurs numériques sont suggérées pour les lettres.En substituant des chiffres à la place des lettres, trouvez la valeur numérique de l'expression résultante.
Comparer les expressions mathématiques
Ces tâches sont variées:
- déterminer l'égalité ou l'inégalité de ces deux expressions (après avoir trouvé et comparé leurs valeurs);
- au rapport donné au signe et à une des expressions pour composer la deuxième expression ou compléter celle proposée inachevée;
- dans de tels exercices, des nombres et des quantités à un chiffre, à deux chiffres, à trois chiffres peuvent être utilisés dans les expressions et les quatre opérations arithmétiques. Le but principal de ces tâches est une solide assimilation du matériel théorique et le développement des compétences informatiques.
- Résoudre les équations. Ils aident à comprendre les liens entre les composants et les résultats des opérations arithmétiques.
- Résoudre le problème Ce peut être des tâches simples et complexes. Avec leur aide, les connaissances théoriques sont renforcées, les compétences en calcul et les compétences sont développées, l'activité mentale des enfants est activée.
Compte oral
Signes de divisibilité des nombres:
- par 2: tout ce qui le dépasse, et dans la rangée numérique en passer un;
- sur 3 et 9: si la somme des chiffres est un multiple de ces indicateurs sans balance;
- par 4: si les deux derniers chiffres de la fiche forment successivement un nombre divisé par 4;
- 5: autour des douzaines et celles où il y a 5 à la fin;
- par 6: les nombres qui sont des multiples de deux et trois sont divisés;
- 10: valeurs numériques dans lesquelles l'enregistrement est à la fin est 0;
- 12: diviser les nombres qui peuvent être divisés en trois et quatre en même temps;
- par 15: nombres divisés en même temps en composantes intégrales à valeur unique de ce nombre facteurs.
Formulaire de compte d'école primaire
Il est bien connu que l'activité principale des enfants d'âge préscolaire et des plus jeunes est un jeu qu'il est utile d'inclure dans toutes les étapes de la leçon. Certaines formes du compte rendu oral seront données ci-dessous.
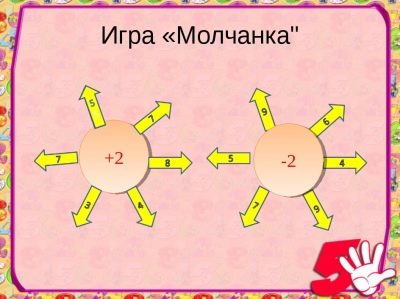
Le jeu "silencieux"
Cela aide à cultiver l'attention et la discipline. Un silence peut consister en des exemples d'une action, deux ou plus. Il est joué dans toutes les classes de l'école primaire avec des nombres entiers abstraits et des nombres nommés.
Les élèves réfléchissent dans leur esprit et silencieusement sur appel, les enseignants écrivent les réponses aux exemples qui leur sont proposés au tableau. Les bonnes réponses se heurtent à des applaudissements légers et les mauvaises réponses à un silence.
Jeu "Loto"
Il peut y avoir plusieurs types correspondant aux sections de mathématiques étudiées et qui doivent être corrigées. Par exemple, loto avec des exemples de multiplication et de division dans les "centaines".
Pour donner plus d’intérêt au jeu, vous pouvez créer des pneus avec des réponses précises. Si tous les exemples sont résolus correctement, une image est faite à partir des pneus.
Jeu "Labyrinthes arithmétiques"
Ils ressemblent à des cercles concentriques avec des portes avec des nombres. Pour vous rendre au centre, vous devez composer un numéro au centre. Les labyrinthes pour la décision peuvent exiger soit une action (addition), soit plusieurs. Il convient de noter que ces tâches ont plusieurs solutions.
Le jeu "Attrapez le pilote" (une sorte d '"échelle")
Sur la planche à dessin: un avion avec des boucles, dans lequel des exemples. Deux étudiants convoqués enregistrent les réponses à gauche et à droite des boucles. Qui décide correctement et rapidement, il va rattraper le pilote.
Le jeu "Exemples circulaires"
Le matériel didactique est un ensemble de cartes, disposées dans des enveloppes; Chacun d'entre eux a 8 cartes, chacune contenant un exemple.
Les exemples numériques de chaque enveloppe ont un contenu différent et sont sélectionnés selon le principe de la maîtrise de soi: pour les résoudre, le résultat d'un exemple sera le début de l'autre.
Des exemples circulaires peuvent être proposés sous forme d'échelles.
Méthodes et techniques de développement
Compte tenu des moyens d’enseigner aux enfants de 6 ans à compter rapidement, il est impossible de ne pas noter le caractère unique et la simplicité de la méthode japonaise de comptage «Soroban». La technique Soroban vous permet de former des enfants âgés de 4 à 11 ans, de développer leurs capacités mentales et d’élargir l’éventail des capacités intellectuelles des enfants.Il est facile d’enseigner à n’importe quel élève de prendre des exemples de mathématiques dans l’esprit, en utilisant la méthode japonaise consistant à compter sur le sorobane. En pratiquant des comptages verbaux mentaux, nous mettons tout le cerveau en action., déchargeant ainsi l’hémisphère gauche, responsable de la résolution des problèmes mathématiques.
L'arithmétique mentale permet même à l'hémisphère «figuratif» de s'intéresser aux opérations de calcul, ce qui augmente l'efficacité du cerveau.
Les grands nombres exigent des méthodes de calcul écrites, bien que certaines personnes perfectionnent leurs compétences pour travailler avec elles.
Considérer des exemples de mathématiques dans l’esprit est une nécessité vitale, étant donné que les examens à l’école ne font maintenant plus appel à des calculatrices, la capacité de compter dans l’esprit est incluse dans la liste des compétences obligatoires pour les diplômés des 9e et 11e années.
La règle de base pour l'addition mentale est la suivante:
- Si le premier terme est un nombre à deux chiffres (et non une douzaine ronde), ajoutez 9 comme suit: ajoutez 10, supprimez 1.
- Ajouter 8: ajouter 10, supprimer 2.
Ajoutez rapidement des nombres à deux chiffres:
- Si le dernier chiffre du second terme est supérieur à 5, arrondissez-le vers le haut. Nous effectuons l'addition, à partir du montant résultant, nous retirons "l'additif".
- Si le dernier chiffre du second terme est inférieur à 5, additionnez-le ensuite: ajoutez d'abord des dizaines, puis - unités.
- Vous pouvez échanger les termes à la place, mais ajouter les nombres en utilisant le même algorithme.
Fonctions de soustraction: réduction aux nombres arrondis
La franchise non équivoque est arrondie à 10, à deux chiffres - jusqu'à 100. Soustrayez 10 ou 100 et ajoutez la modification. La réception est pertinente pour les petits amendements.
Soustrayez les nombres à trois chiffres à l'esprit
Sur la base d’une bonne connaissance de la composition des nombres des dix premiers, vous pouvez soustraire des parties dans cet ordre: des centaines, des dizaines, des unités.
Multiplier et diviser peuvent se faire facilement, en connaissant le tableau de multiplication - «baguette magique» pour le développement rapide du compte à l’esprit. Il est à noter que les enfants du village de la Russie prérévolutionnaire connaissaient le maintien de la soi-disant table de Pythagore - de 11 à 19 ans - et il serait bien que les érudits modernes connaissent la table par cœur jusqu'à 19 * 9.
Les astuces les plus intéressantes
Pour captiver les enfants avec les mathématiques et rendre les moments difficiles du programme scolaire plus proches et plus accessibles, il existe des moyens et des méthodes, Transformer les difficultés en divertissement et intéressant:
- Pour multiplier un chiffre par 9, montrons à tous nos mains vides. Pliez votre doigt, en respectant l'ordre (en partant du pouce de la main gauche) avec le numéro du premier facteur. Nous regardons combien de doigts se trouvent à gauche de la courbe - ce seront des dizaines du travail souhaité, et à droite - sa propre unité.
- Multiplier par 11 tout nombre à deux chiffres, dont la somme n’atteint pas 10, est simple et amusant: déplacez mentalement les chiffres de ce nombre et mettez leur somme entre eux - la réponse est prête.
- Si la somme des chiffres multipliée par 11 s'avère être 10 ou plus de 10, vous devez mettre leur somme entre les chiffres espacés mentalement de ce nombre et ajouter les deux premiers chiffres à gauche, en laissant les deux autres inchangés, pour obtenir le produit.
Pour savoir comment apprendre à votre enfant à compter instantanément dans votre esprit, voyez la vidéo suivante.