अपने दिमाग में जल्दी से गिनती करने के लिए एक बच्चा कैसे सीखें?
ईर्ष्या वाले आधुनिक बच्चों के माता-पिता गीक्स देख रहे हैं - टेलीविजन शो "बेस्ट ऑफ ऑल" और "अमेजिंग पीपल" के प्रतिभागी - और चिंता करें कि उनके बच्चे उनकी उत्कृष्ट बुद्धिमत्ता और सुपर-विट के लिए प्रतिष्ठित नहीं हैं: वे खराब प्राथमिक विद्यालय कार्यक्रम सीखते हैं, वे अपने दिमाग को तनाव में रखना पसंद नहीं करते और सबक से डरते हैं। गणित।
पहली कक्षा से वे उंगलियों और वैंड पर भरोसा करते हैं, वे मौखिक गिनती की तकनीक नहीं जानते हैं, इसलिए उन्हें स्कूल पाठ्यक्रम के सभी विषयों में बड़ी समस्याएं हैं।
त्वरित मौखिक गिनती की तकनीक सरल और आसानी से पच जाती है, लेकिन यह याद रखना चाहिए कि उनमें से सफल महारत का अर्थ यांत्रिक नहीं, बल्कि तकनीकों के प्रति काफी सचेत उपयोग और इसके अलावा, कम या ज्यादा लंबा प्रशिक्षण भी है।
मौखिक खाते के प्रारंभिक तरीकों में महारत हासिल करने के बाद, उनका उपयोग सही ढंग से और जल्दी से लिखित गणना के साथ सटीकता के साथ मन में त्वरित गणना करने में सक्षम होगा।
विशेष सुविधाएँ
ऐसी कई तकनीकें हैं जो मानसिक गणित को गति देने के लिए सीखने को बढ़ावा देती हैं। सभी दृश्यमान अंतरों के साथ, उनके पास एक महत्वपूर्ण समानता है - वे तीन "व्हेल" पर आधारित हैं:
- प्रशिक्षण और अनुभव का संचय। नियमित अभ्यास, सरल से जटिल गुणात्मक और मात्रात्मक रूप से कार्यों का समाधान मौखिक गणना के कौशल को बदलता है।
- एल्गोरिथ्म। "गुप्त" विधियों और कानूनों का ज्ञान और अनुप्रयोग गिनती की प्रक्रिया को बहुत सरल करता है।
- क्षमताओं और प्राकृतिक बंदोबस्ती। अल्पकालिक स्मृति और इसकी काफी मात्रा, साथ ही ध्यान की उच्च एकाग्रता विकसित - एक त्वरित मानसिक अंकगणित का अभ्यास करने में एक बड़ी मदद। एक निश्चित प्लस एक गणितीय मानसिकता की उपस्थिति और तार्किक सोच की एक प्रवृत्ति है।
मौखिक खाते का उपयोग
लोग लोहे के रोबोट नहीं हैं, लेकिन यह तथ्य है कि वे स्मार्ट मशीन बनाते हैं, उनकी बौद्धिक श्रेष्ठता की बात करते हैं। एक व्यक्ति को लगातार अपने मस्तिष्क को अच्छे आकार में रखने की आवश्यकता होती है, जिसे मानसिक अंकगणित में कौशल के प्रशिक्षण द्वारा सक्रिय रूप से बढ़ावा दिया जाता है।
रोजमर्रा की जिंदगी के लिए:
- एक सफल मौखिक खाता एक विश्लेषणात्मक मानसिकता का एक संकेतक है;
- नियमित मानसिक अंकगणित आपको प्रारंभिक मनोभ्रंश और उपजाऊ मारमास से बचाएगा;
- अच्छी तरह से जोड़ने और घटाने की आपकी क्षमता आपको स्टोर में धोखा देने की अनुमति नहीं देगी।
सफल अध्ययन के लिए:
- मानसिक गतिविधि सक्रिय है;
- स्मृति का विकास, भाषण, ध्यान, सुनने की क्षमता, सुनने की क्षमता, प्रतिक्रिया की गति, सरलता, समस्या को हल करने के सबसे तर्कसंगत तरीके खोजने की क्षमता;
- उनकी क्षमताओं पर विश्वास मजबूत किया।
मुझे अपनी पढ़ाई कब शुरू करनी चाहिए?
सीखे हुए दिमागों (मनोवैज्ञानिकों और शिक्षकों) के अनुसार, 4 साल का बच्चा पहले से ही जोड़ और घटा सकता है। 5 वर्ष की आयु तक, क्रंब स्वतंत्र रूप से उदाहरणों और सरल कार्यों को हल कर सकता है। लेकिन यह आंकड़े हैं, और बच्चे हमेशा इसके अनुकूल नहीं होते हैं। इसलिये यहाँ सब कुछ विशुद्ध रूप से व्यक्तिगत है।
किसी भी मामले में, बच्चों को स्कूल में प्रवेश करने से पहले उनके दिमाग में जल्दी से गिनती करना सिखाना बेहतर है - कम समस्याएं होंगी, और उपयोगी कौशल की आपूर्ति से आधुनिक स्कूल कार्यक्रमों को अधिक सफलतापूर्वक मास्टर करने में मदद मिलेगी।
नियम
विज्ञान की रानी - गणित - छात्रों का ध्यान रखा और कानून का एक सेट बनाया, एल्गोरिदम और नियम, महारत हासिल करने और कुशलता से उनका उपयोग करना, बच्चों को गणित और मानसिक काम पसंद आएगा:
- जोड़ की हस्तांतरण संपत्ति: कार्रवाई के घटकों को स्वैप करना, हमें एक ही परिणाम मिलता है।
- संयुक्त जोड़ संपत्ति: जब तीन या अधिक संख्याओं को एक साथ जोड़ा जाता है, तो किसी भी दो (या अधिक) संख्यात्मक मानों को उनकी राशि से बदला जा सकता है।
- एक दर्जन के माध्यम से संक्रमण के साथ जोड़ और घटाव: एक बड़ा घटक जोड़ें
- दर्जनों राउंड के लिए, और फिर अन्य घटक के शेष जोड़ें।
- पहले व्यक्तिगत इकाइयों को संख्या से कार्रवाई के संकेत तक घटाएं, और फिर दर्जनों राउंड से हम घटाए गए शेष को घटाते हैं।
- दसियों और इकाइयों के योग के रूप में कम प्रस्तुत करने के बाद, हम दसियों बड़े से छोटे को हटाते हैं और घटते हुए इकाइयों के उत्तर में जोड़ते हैं।
- दर्जनों राउंड को जोड़ने और घटाने पर (उन्हें अभी भी "राउंड" नंबर कहा जाता है), दर्जनों को इकाइयों के समान माना जा सकता है।
- दसियों और इकाइयों का जोड़ और घटाव। दसियों को जोड़ने के लिए दर्जनों अधिक सुविधाजनक है, और इकाइयों - इकाइयों के लिए।
राशि में एक संख्या जोड़ रहा है
विधियाँ इस प्रकार हैं:
- हम इसके मूल्य की गणना करते हैं, और फिर इस मूल्य को इसमें जोड़ते हैं।
- हम इसे पहले कार्यकाल में जोड़ते हैं, और फिर हम परिणाम में दूसरा शब्द जोड़ते हैं।
- हम संख्या को दूसरे शब्द में जोड़ते हैं, और फिर उत्तर में पहला शब्द जोड़ते हैं।
संख्या के लिए राशि का जोड़
विधियाँ इस प्रकार हैं:
- हम इसकी गवाही की गणना करते हैं, और फिर हम संख्या में जोड़ते हैं।
- हम संख्या में पहला शब्द जोड़ते हैं, और फिर हम परिणाम में दूसरा शब्द जोड़ते हैं।
- हम संख्या में दूसरा शब्द जोड़ते हैं, और फिर हम परिणाम में पहला शब्द जोड़ते हैं।
दो राशियों का जोड़। दो रकम जोड़कर, हम गणना करने के लिए सबसे सुविधाजनक तरीका चुनते हैं।
मुख्य गुणन गुणों का उपयोग करना
तकनीक इस प्रकार हैं:
- गुणन की हस्तांतरण संपत्ति। यदि हम कारकों को स्थानों में बदलते हैं, तो उनका उत्पाद नहीं बदलेगा।
- गुणन की संयुक्त संपत्ति। तीन या अधिक संख्याओं को गुणा करते समय, किसी भी दो (या अधिक) संख्याओं को उनके उत्पाद द्वारा प्रतिस्थापित किया जा सकता है।
- गुणन का वितरण गुण। किसी संख्या द्वारा योग को गुणा करने के लिए, इसके प्रत्येक घटक को इस संख्या से गुणा करना और परिणामी कार्यों को जोड़ना आवश्यक है।
गुणा और संख्या को 10 और 100 से विभाजित करें
तरीके:
- किसी भी संख्या को 10 गुना बढ़ाने के लिए, आपको दाईं ओर एक शून्य जोड़ना होगा।
- ऐसा 100 बार करने के लिए, दो शून्य को दाईं ओर सौंपा जाना चाहिए।
- संख्या को 10 गुना कम करने के लिए, आपको एक शून्य को दाईं ओर गिराना होगा, और 100 - दो शून्य से विभाजित करना होगा।
राशि को संख्या से गुणा करें
तरीके:
- पहली विधि। राशि की गणना करें और इसे इस मूल्य से गुणा करें।
- दूसरा तरीका। प्रत्येक जोड़ के साथ संख्या गुणा करें, और प्राप्त उत्तर जोड़ें।
राशि से गुणा संख्या
तरीके:
- पहली विधि। योग प्राप्त करें और हमें प्राप्त होने वाली संख्या को गुणा करें।
- दूसरा तरीका। प्रत्येक जोड़ द्वारा संख्या गुणा करें, और परिणामी कार्यों को जोड़ें।
राशि को संख्या से विभाजित करना
तरीके:
- पहली विधि। राशि की गणना करें और इसे एक संख्या से विभाजित करें।
- दूसरा तरीका। प्रत्येक जोड़ संख्या से विभाजित होता है और परिणामी उद्धरण जोड़े जाते हैं।
उत्पाद की संख्या को विभाजित करना
विकल्प:
- पहली विधि। पहले कारक द्वारा संख्या को विभाजित करें, और फिर दूसरे कारक द्वारा परिणाम को विभाजित करें।
- दूसरा तरीका। संख्या को दूसरे कारक से विभाजित करें, और फिर परिणाम को पहले कारक से विभाजित करें।
प्रकार
मौखिक खाते में पाठों में समय के लिए डरावना समय दिया जाता है, लेकिन यह बच्चों की मानसिक गतिविधि के विकास के लिए इसके महत्व को नहीं रोकता है। विभिन्न प्रकार के कार्यों और अभ्यासों को निष्पादित करते समय प्राथमिक विद्यालय में गणित के पाठों में मौखिक कम्प्यूटेशनल कौशल का गठन किया जाता है।
गणित की अभिव्यक्ति का मान ज्ञात कीजिए
ये एक चर (वर्णमाला) के साथ साधारण संख्यात्मक अभिव्यक्तियाँ या भाव हो सकते हैं, और अक्षरों के लिए संख्यात्मक मान सुझाए जाते हैं।अक्षरों के बजाय संख्याओं को प्रतिस्थापित करते हुए, परिणामी अभिव्यक्ति का संख्यात्मक मान ज्ञात करें।
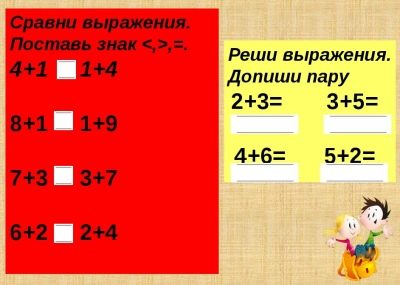
गणित अभिव्यक्तियों की तुलना करें
ऐसे कार्य विविध हैं:
- इन दो अभिव्यक्तियों की समानता या असमानता का निर्धारण (उनके मूल्यों को खोजने और तुलना करने के बाद);
- दूसरी अभिव्यक्ति की रचना करने और अधूरे प्रस्तावित एक को पूरा करने के लिए संकेत और एक अभिव्यक्ति को दिए गए संबंध में;
- ऐसे अभ्यासों में, एकल-अंक, दो-अंक, तीन-अंकों की संख्या और मात्रा का उपयोग अभिव्यक्तियों और सभी चार अंकगणितीय कार्यों में किया जा सकता है। इस तरह के कार्यों का मुख्य उद्देश्य सैद्धांतिक सामग्री और कम्प्यूटेशनल कौशल के विकास का एक ठोस आत्मसात है।
- समीकरणों को हल करें। वे घटकों और अंकगणितीय संचालन के परिणामों के बीच संबंधों को समझने में मदद करते हैं।
- समस्या का समाधान करें। यह सरल और जटिल दोनों कार्य हो सकते हैं। उनकी मदद से, सैद्धांतिक ज्ञान को मजबूत किया जाता है, कम्प्यूटेशनल कौशल और कौशल विकसित किए जाते हैं, बच्चों की मानसिक गतिविधि सक्रिय होती है।
मौखिक खाता रिसेप्शन
संख्याओं की विभाज्यता के संकेत:
- 2: सभी जो इसे पार करते हैं, और संख्यात्मक पंक्ति में एक से गुजरते हैं;
- 3 और 9 पर: यदि अंकों का योग संतुलन के बिना इन संकेतकों का एक बहु है;
- 4 से: यदि रिकॉर्ड में अंतिम दो अंक क्रमिक रूप से एक संख्या बनाते हैं जो 4 से विभाजित होता है;
- 5: राउंड दर्जनों और जहां अंत में 5 है;
- 6: संख्या जो दो और तीन के गुणक हैं, विभाजित हैं;
- 10: संख्यात्मक मान, जिसमें अंत में रिकॉर्ड 0 है;
- 12: उन संख्याओं को विभाजित करें जिन्हें एक ही समय में तीन और चार में विभाजित किया जा सकता है;
- 15 तक: संख्या जो इस संख्या कारकों के एकल-मूल्यवान अभिन्न घटकों में एक ही समय में विभाजित होती है।
प्राथमिक विद्यालय खाता प्रपत्र
यह सर्वविदित है कि पूर्वस्कूली और छोटे छात्रों की मुख्य गतिविधि एक ऐसा खेल है जो पाठ के सभी चरणों में शामिल करने के लिए उपयोगी है। मौखिक खाते के कुछ रूप नीचे दिए जाएंगे।
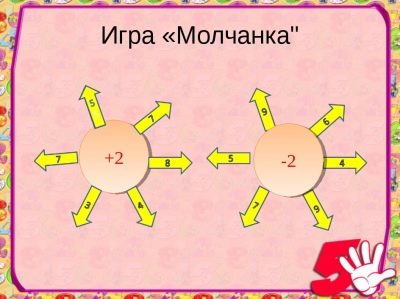
खेल "मौन"
यह ध्यान और अनुशासन की खेती करने में मदद करता है। एक मौन में एक क्रिया में दो या अधिक उदाहरण हो सकते हैं। यह प्राथमिक विद्यालय के सभी वर्गों में सार पूर्णांक और नामित संख्या दोनों के साथ खेला जाता है।
छात्र अपने मन में और चुपचाप कॉल पर विचार करते हैं, शिक्षक ब्लैकबोर्ड पर उन्हें दिए गए उदाहरणों के उत्तर लिखते हैं। सही जवाब हल्के ताली के साथ मिलते हैं, और गलत जवाब चुप्पी के साथ।
खेल "लोट्टो"
गणित के उन वर्गों के अनुरूप कई प्रकार हो सकते हैं जिनका अध्ययन किया जाता है और उन्हें ठीक करने की आवश्यकता होती है। उदाहरण के लिए, "सैकड़ों" के भीतर गुणा और विभाजन के उदाहरणों के साथ लोट्टो।
खेल को अधिक रुचि देने के लिए, कटे हुए चित्र से उत्तरों के साथ टायर बनाए जा सकते हैं। यदि सभी उदाहरणों को सही ढंग से हल किया जाता है, तो टायर से एक तस्वीर बनाई जाती है।
खेल "अंकगणित भूलभुलैया"
वे संख्याओं के साथ फाटकों के साथ गाढ़ा हलकों की तरह दिखते हैं। केंद्र पर जाने के लिए, आपको केंद्र में एक नंबर डायल करना होगा। निर्णय के लिए लेबिरिंथ या तो एक कार्रवाई (अतिरिक्त), या कई मांग कर सकते हैं। यह ध्यान दिया जाना चाहिए कि इन कार्यों के कई समाधान हैं।
खेल "पायलट को पकड़ो" (एक प्रकार की "सीढ़ी")
ड्राइंग बोर्ड पर: छोरों के साथ एक विमान, जिसमें उदाहरण हैं। दो बुलाए गए छात्रों ने छोरों के बाईं और दाईं ओर प्रतिक्रियाएं दर्ज कीं। जो सही ढंग से और जल्दी से फैसला करता है, वह पायलट के साथ पकड़ लेगा।
खेल "परिपत्र उदाहरण"
डिडैक्टिक सामग्री कार्ड का एक सेट है, जो लिफाफे में व्यवस्थित है; उनमें से प्रत्येक में 8 कार्ड हैं, जिनमें से प्रत्येक में एक उदाहरण है।
प्रत्येक लिफाफे में संख्यात्मक उदाहरण सामग्री में भिन्न होते हैं और आत्म-नियंत्रण के सिद्धांत के अनुसार चुने जाते हैं: उन्हें हल करने में, एक उदाहरण का परिणाम अगले की शुरुआत होगी।
परिपत्र उदाहरण को सीढ़ी के रूप में पेश किया जा सकता है।
विकास के तरीके और तकनीक
6 साल के बच्चों को उनके दिमाग में त्वरित गिनती सिखाने के तरीकों को ध्यान में रखते हुए, "सोरोबान" की गिनती के जापानी तरीके की विशिष्टता और सादगी को नोट करना मुश्किल नहीं है। सोरोबान तकनीक आपको 4 से 11 वर्ष की आयु के बच्चों को प्रशिक्षित करने, उनकी मानसिक क्षमताओं को विकसित करने और बच्चों की बौद्धिक क्षमताओं की सीमा का विस्तार करने की अनुमति देती है।किसी भी छात्र को गणित के उदाहरणों को मन में लेने के लिए सिखाना आसान है, सोर्बोन पर गिनती के जापानी तरीके का उपयोग करना। मानसिक मौखिक गणना का अभ्यास करके, हम पूरे मस्तिष्क को ऑपरेशन में लगाते हैं।, जिससे बाईं गोलार्ध को उतार दिया जाता है, जो गणितीय समस्याओं को हल करने के लिए जिम्मेदार है।
मानसिक अंकगणित भी "लाक्षणिक" गोलार्द्ध को कम्प्यूटेशनल संचालन में रुचि रखने की अनुमति देता है, जिससे मस्तिष्क की दक्षता बढ़ जाती है।
बड़ी संख्या में गणना के लिखित तरीकों की आवश्यकता होती है, हालांकि ऐसे व्यक्ति हैं जो उनके साथ काम करने में अपने कौशल को सुधारते हैं।
मन में गणित के उदाहरणों पर विचार करना एक महत्वपूर्ण आवश्यकता है, चूँकि स्कूल में परीक्षा अब कैलकुलेटर के उपयोग के बिना होती है, और मन में गिनने की क्षमता 9 और 11 ग्रेड के स्नातकों के अनिवार्य कौशल की सूची में शामिल है।
मानसिक जोड़ के लिए मूल नियम है:
- यदि पहला शब्द दो अंकों की संख्या है (एक राउंड दर्जन नहीं), तो इसमें 9 को इस प्रकार जोड़ें: 10 जोड़ें, 1 निकालें।
- 8 जोड़ें: 10 जोड़ें, 2 निकालें।
जल्दी से दो अंकों की संख्या जोड़ें:
- यदि दूसरे पद का अंतिम अंक 5 से अधिक है, तो इसे ऊपर की ओर गोल करें। हम अतिरिक्त जोड़ते हैं, परिणामस्वरूप राशि से हम "एडिटिव" को हटाते हैं।
- यदि दूसरे शब्द का अंतिम अंक 5 से कम है, तो अंकों से जोड़ें: पहले, दर्जनों जोड़ो, फिर इकाइयों।
- आप स्थानों में शर्तों को स्वैप कर सकते हैं, लेकिन समान एल्गोरिथ्म का उपयोग करके संख्याओं को जोड़ सकते हैं।
घटाव सुविधाएँ: गोल संख्या में कमी
असंदिग्ध घटाया को 10, दो-अंक - 100 तक - 10 तक घटाया जाता है और संशोधन जोड़ा जाता है। रिसेप्शन छोटे संशोधनों के लिए प्रासंगिक है।
तीन अंकों की संख्या को ध्यान में रखते हुए घटाएं
पहले दस की संख्या की संरचना के अच्छे ज्ञान के आधार पर, आप इस क्रम में भागों में घटा सकते हैं: सैकड़ों, दसियों, इकाइयाँ।
गुणा और भाग आसानी से हो सकता है, गुणन तालिका को जानकर - "जादू की छड़ी" खाते के तेजी से विकास को ध्यान में रखते हुए। यह उल्लेखनीय है कि पूर्व-क्रांतिकारी रूस के गांव के बच्चे 11 से 19 तक तथाकथित पाइथोगोरियन तालिका की निरंतरता जानते थे, और आधुनिक विद्वानों के लिए यह हृदय से 19 * 9 तक की तालिका जानना अच्छा होगा।
सबसे दिलचस्प टोटके
गणित के साथ बच्चों को लुभाने और स्कूल के पाठ्यक्रम में कठिन क्षणों को करीब और अधिक सुलभ बनाने के लिए, तरीके और तरीके हैं, कठिनाइयों को मज़ेदार और दिलचस्प में बदलना:
- किसी भी एक अंक को 9 से गुणा करने के लिए, सभी को अपनी खाली हथेलियाँ दिखाएँ। अपनी उंगली को मोड़ें, क्रम में (बाएं हाथ के अंगूठे से गिनती) पहले कारक की संख्या तक। हम देखते हैं कि तुला के बाईं ओर कितनी उंगलियां हैं - यह वांछित काम के दर्जनों होंगे, और दाईं ओर - अपनी स्वयं की इकाई।
- किसी भी दो अंकों की संख्या के 11 से गुणा, जिसका योग 10 तक नहीं पहुंचता है, मजेदार और सरल है: मानसिक रूप से इस संख्या के अंकों को स्थानांतरित करें और उनके बीच अपनी राशि डालें - जवाब तैयार है।
- यदि अंकों का योग 11 से गुणा होकर 10 या 10 से अधिक हो जाता है, तो इस संख्या के मानसिक रूप से कम अंकों के बीच में आपको अपना योग डालना चाहिए और पहले दो अंकों को बाईं ओर जोड़ना चाहिए, अन्य दो को अपरिवर्तित, उत्पाद प्राप्त करने के लिए।
अपने मन में तुरन्त गिनती करने के लिए अपने बच्चे को कैसे सिखाना है, इसकी जानकारी के लिए, निम्न वीडियो देखें।