Kako naučiti dijete da brzo broji u glavi?
Roditelji moderne djece s zavišću promatraju geekove - sudionike televizijske emisije "Najbolje od svih" i "nevjerojatne ljude" - i brinu da se njihova djeca ne razlikuju izvanrednom inteligencijom i duhovitošću: ne ovladaju programom osnovne škole, ne vole naprezati mozak i boje se lekcija matematika.
Od prvog razreda računaju na prste i štapiće, ne poznaju tehnike oralnoga brojanja, stoga imaju velike probleme u svim predmetima školskog tečaja.
Tehnike brzog oralnog brojanja su jednostavne i lako probavljive, ali treba imati na umu da uspješno ovladavanje njima ne uključuje mehaničko, već sasvim svjesno korištenje tehnika i, uz to, više ili manje dugotrajnu obuku.
Nakon što su ovladali elementarnim metodama usmene obrade, pomoću njih ćete moći ispravno i brzo izvesti trenutne izračune u umu s istom točnošću kao i kod pisanih izračuna.
Značajke
Postoji mnogo tehnika koje potiču učenje kako bi se ubrzala mentalna aritmetika. Uz sve vidljive razlike, one imaju važnu sličnost - temelje se na tri "kitova":
- Obuka i akumulacija iskustva. Redovita praksa, rješavanje zadataka od jednostavne do složene kvalitativno i kvantitativno mijenja vještinu usmenog računanja.
- Algoritam. Poznavanje i primjena "tajnih" metoda i zakona uvelike pojednostavljuje proces brojanja.
- Sposobnosti i prirodne zaklade. Razvijena kratkotrajna memorija i njen značajan volumen, kao i visoka koncentracija pažnje - velika pomoć u prakticiranju brze mentalne aritmetike. Definitivni plus je prisutnost matematičkog načina razmišljanja i predispozicije za logično razmišljanje.
Korištenje usmenog računa
Ljudi nisu željezni roboti, ali činjenica da stvaraju pametne strojeve govori o njihovoj intelektualnoj superiornosti. Osoba treba stalno držati svoj mozak u dobroj formi, što se aktivno promiče obukom vještina u mentalnoj aritmetici.
Za svakodnevni život:
- uspješan usmeni račun pokazatelj je analitičkog razmišljanja;
- redovita mentalna aritmetika spasit će vas od rane demencije i senilnog marazma;
- Vaša sposobnost da dodajete i oduzimate dobro neće vam dopustiti da varate u trgovini.
Za uspješno učenje:
- aktivira se mentalna aktivnost;
- razviti memorijugovor, pažnja, sposobnost opažanja onoga što je rečeno na slušanju, brzina reakcije, domišljatost, sposobnost pronalaženja najracionalnijih načina za rješavanje problema;
- ojačali povjerenje u njihove sposobnosti.
Kada trebam započeti studij?
Prema znanstvenim umovima (psiholozima i odgajateljima), dijete do 4. godine već može dodati i oduzeti. Do dobi od 5 godina, mrvica može slobodno rješavati primjere i jednostavne zadatke. Ali to je statistika, a djeca se ne prilagođavaju uvijek. stoga sve je ovdje čisto individualno.
U svakom slučaju, bolje je naučiti djecu da brzo računaju u svoj um prije nego što uđu u školu - bit će manje problema, a zalihe korisnih vještina pomoći će uspješnije savladavanje suvremenih školskih programa.
pravila
Kraljica znanosti - matematika - brinula se o studentima i izradila set zakona, Algoritmi i pravila, nakon što ih ovladaju i vješto koriste, djeca će voljeti matematiku i mentalni rad:
- Prijenosno svojstvo dodatka: zamjena komponenti akcije, dobivamo isti rezultat.
- Kombinirano svojstvo dodavanja: kada se zbroje tri ili više brojeva, bilo koje dvije (ili više) brojčane vrijednosti mogu se zamijeniti njihovim zbrojem.
- Dodavanje i oduzimanje s prijelazom kroz desetak: dodajte veću komponentu
- Za desetke okruglih, a zatim dodajte ostatak druge komponente.
- Prvo oduzimamo pojedinačne jedinice od broja do znaka akcije, a zatim iz desetaka rundi oduzimamo ostatak odbitne stavke.
- Predstavivši umanjen u obliku zbroja desetaka i jedinica, uklanjamo iz desetaka veće i manje i dodajemo odgovoru jedinice umanjenja.
- Kada se zbrajaju i oduzimaju desetine rundi (još uvijek se nazivaju "okruglim" brojevima), desetine se mogu smatrati jednakima jedinicama.
- Dodavanje i oduzimanje desetaka i jedinica. Deseci više zgodan dodati desetaka, a jedinice - na jedinice.
Dodajte broj u iznos
Metode su sljedeće:
- Izračunavamo njegovu vrijednost, a zatim joj dodajemo zadanu vrijednost.
- Dodamo je prvom terminu, a zatim rezultatu dodamo drugi pojam.
- Dodamo broj drugom terminu, a zatim odgovoru dodamo prvi pojam.
Dodavanje iznosa broju
Metode su sljedeće:
- Izračunajte njezino svjedočanstvo, a zatim dodajte broj.
- Dodamo prvi pojam broju, a zatim rezultatu dodamo drugi pojam.
- Dodamo drugi pojam broju, a zatim rezultatu dodamo prvi pojam.
Dodavanje dva iznosa. Dodavanjem dva iznosa odabiremo najpogodniji način izračuna.
Korištenje glavnih svojstava množenja
Tehnike su sljedeće:
- Prijenosno svojstvo množenja. Ako mijenjamo faktore na mjestima, njihov proizvod se neće promijeniti.
- Kombinirano svojstvo množenja. Kada množite tri ili više brojeva, bilo koja dva (ili više) brojeva mogu se zamijeniti njihovim proizvodom.
- Distribucijsko svojstvo množenja. Kako bi zbroj pomnožili brojem, potrebno je pomnožiti svaku od njegovih sastavnica s tim brojem i dodati dobivene radove.
Pomnožite i podijelite brojeve za 10 i 100
metode:
- Da biste povećali bilo koji broj za 10 puta, morate dodati jednu nulu udesno.
- Da bi se učinilo isto 100 puta, dvije nule moraju biti dodijeljene desno.
- Da biste smanjili broj za 10 puta, morate spustiti jednu nulu udesno i podijeliti sa 100 - dvije nule.
Pomnožite iznos s brojem
metode:
- 1. metoda. Izračunajte iznos i pomnožite ga s ovom vrijednošću.
- 2. put. Pomnožite broj sa svakim dodatkom i dodajte dobivene odgovore.
Pomnožite broj po sumi
metode:
- 1. metoda. Pronađite sumu i pomnožite broj prema onome što dobijemo.
- 2. put. Pomnožite broj za svaki dodatak i dodajte dobivene radove.
Podijelite iznos s brojem
metode:
- 1. metoda. Izračunajte iznos i podijelite ga s brojem.
- 2. put. Svaki od dodataka je podijeljen na brojeve i dodani su koeficijenti.
Podjela broja proizvoda
opcije:
- 1. metoda. Podijelite broj s prvim čimbenikom, a zatim ga podijelite s drugim čimbenikom.
- 2. put. Podijelite broj s drugim čimbenikom, a zatim ga podijelite s prvim čimbenikom.
vrste
Tijekom nastave oskudno se vrijeme pripisuje usmenom iskazu, ali to ne umanjuje njegovu važnost za razvoj mentalne aktivnosti djece. U nastavi matematike u osnovnoj školi formiraju se usmene računalne vještine pri izvođenju različitih vrsta zadataka i vježbi.
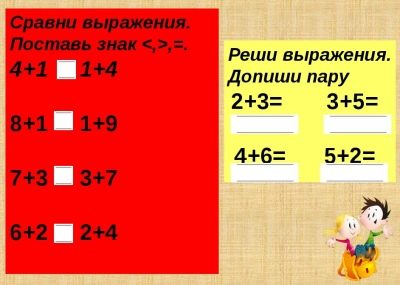
Pronađite vrijednost matematičkog izraza
To mogu biti obični numerički izrazi ili izrazi s varijablom (abecedno), a za slova se predlažu numeričke vrijednosti.Zamjenjujući brojeve umjesto slova, pronađite brojčanu vrijednost dobivenog izraza.
Usporedite matematičke izraze
Takvi zadaci su različiti:
- odrediti jednakost ili nejednakost dvaju navedenih izraza (prethodno su pronašli i usporedili njihove vrijednosti);
- na odnos dan znak i jedan od izraza za sastavljanje drugog izraza ili za dovršenje nedovršenog predloženog;
- u takvim vježbama mogu se upotrijebiti jednoznamenkaste, dvoznamenkaste, troznamenkaste brojeve i količine u izrazima i sve četiri aritmetičke operacije. Glavna svrha takvih zadataka je čvrsto ovladavanje teorijskim materijalom i razvoj računalnih vještina.
- Riješite jednadžbu. Oni pomažu u razumijevanju odnosa između komponenti i rezultata aritmetičkih operacija.
- Riješite problem. To mogu biti jednostavni i složeni zadaci. Uz njihovu pomoć jačaju se teorijska znanja, razvijaju se računalne vještine i vještine, aktivira mentalna aktivnost djece.
Usmeni prijeme
Znakovi djeljivosti brojeva:
- sa 2: sve što ga nadilazi, au numeričkom nizu prolaze kroz jednu;
- na 3 i 9: ako je zbroj znamenki višekratnik tih pokazatelja bez ravnoteže;
- sa 4: ako posljednje dvije znamenke u zapisu sukcesivno oblikuju broj koji je podijeljen s 4;
- 5: oko desetaka i onih na kojima je 5 na kraju;
- 6: brojevi koji su višestruki od dva i tri su podijeljeni;
- 10: brojčane vrijednosti u kojima je zapis na kraju 0;
- 12: podijelite brojeve koji se mogu podijeliti u tri i četiri u isto vrijeme;
- s 15: brojevi koji su istovremeno podijeljeni pojedinačnim cjelobrojnim komponentama tog broja su množitelji.
Obrasci računa u osnovnoj školi
Poznato je da je glavna aktivnost predškolaca i mlađih učenika igra koja je korisna za uključivanje u sve faze lekcije. Neki oblici usmenog iskaza dat će se u nastavku.
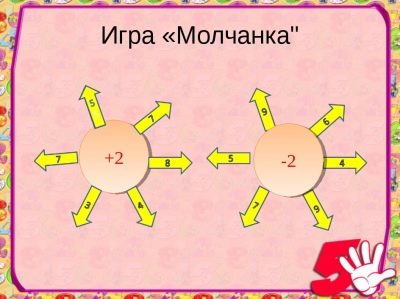
Igra "Tiho"
Promiče obrazovanje i obrazovanje o disciplini. Tišina se može sastojati od primjera u jednoj akciji, dva ili više. Igra se u svim razredima osnovne škole s apstraktnim cijelim brojevima i imenovanim brojevima.
Učenici u svojim mislima i tiho pozivaju učitelje da pišu odgovore na ponuđene primjere na ploči. Točni odgovori susreću se sa laganim pljeskanjem, a pogrešni odgovori tišinom.
Igra "Loto"
Može postojati nekoliko tipova koji odgovaraju onim dijelovima matematike koji se proučavaju i trebaju biti fiksirani. Na primjer, loto s primjerima množenja i podjele unutar "stotina".
Da bi se više zanimalo igri, gume s odgovorima mogu se izraditi iz rezane slike. Ako su svi primjeri ispravno riješeni, slika je napravljena od guma.
Igra "Aritmetički labirinti"
Izgledaju kao koncentrični krugovi s vratima s brojevima. Da biste došli do centra, morate birati broj u sredini. Labirinti za rješenje mogu zahtijevati ili jedno djelovanje (dodavanje) ili nekoliko njih. Treba napomenuti da ove zadaće imaju nekoliko rješenja.
Igra "Uhvatite pilota" (vrsta "ljestve")
Na ploči za crtanje: ravnina s petljama, u kojim primjerima. Dva pozvana studenta bilježe odgovore s lijeve i desne strane petlji. Tko ispravno i brzo odluči, uhvatit će se s pilotom.
Igra "Kružni primjeri"
Didaktički materijal je skup karata, raspoređenih u omotnice; Svaka od njih ima 8 karata od kojih svaka sadrži jedan primjer.
Brojčani primjeri u svakoj omotnici su različiti po svom sadržaju i odabiru se prema načelu samokontrole: pri njihovom rješavanju rezultat jednog primjera bit će početak sljedećeg.
Kružni primjeri mogu se ponuditi kao ljestve.
Metode i tehnike razvoja
Uzimajući u obzir načine kako učiti djecu od 6 godina brzom računanju u svom umu, nemoguće je ne zapaziti jedinstvenost i jednostavnost japanske metode brojanja "Soroban". Metoda "Soroban" omogućuje vam osposobljavanje djece u dobi od 4 do 11 godina, razvijanje njihovih mentalnih sposobnosti i širenje raspona intelektualnih sposobnosti djece.Lako je učiti bilo kojeg učenika da uzme primjere matematike u umu koristeći japansku metodu brojanja sorobana. Prakticirajući mentalne verbalne brojeve, stavljamo cijeli mozak u pogon.i time istovariti lijevu polutku, koja je odgovorna za rješavanje matematičkih problema.
Mentalna aritmetika omogućuje čak i "figurativnoj" hemisferi da budu zainteresirani za računalne operacije, što povećava učinkovitost mozga.
Veliki brojevi zahtijevaju pisane metode proračuna, iako postoje pojedinci koji usavršavaju svoje vještine u radu s njima.
Čitanje matematičkih primjera u umu je vitalna potreba, budući da su ispiti u školi sada bez uporabe kalkulatora, a sposobnost prebrojavanja u um uključena je u popis obveznih vještina diplomiranih studenata 9 i 11 razreda.
Osnovno pravilo za mentalno dodavanje je:
- Ako je prvi pojam dvoznamenkasti broj (ne okrugli broj), tada mu dodajte 9 kako slijedi: dodajte 10, uklonite 1.
- Dodati 8: dodati 10, ukloniti 2.
Brzo dodajte dvoznamenkaste brojeve:
- Ako je zadnja znamenka drugog pojma veća od 5, zaokružite je. Izvršite dodavanje, uklonite "aditiv" iz primljene količine.
- Ako je zadnja znamenka drugog pojma manja od 5, tada se zbrajaju znamenke: prvo, dodajte desetke, a zatim - jedinice.
- Možete mijenjati pojmove na mjestima, ali dodajte brojeve koristeći isti algoritam.
Značajke oduzimanja: smanjenje na okrugle brojeve
Jednoznačni odbitak se zaokružuje na 10, dvoznamenkasti - do 100. Oduzmite 10 ili 100 i dodajte izmjenu. Prijem je relevantan za male izmjene.
Oduzmite tri znamenke u obzir
Na temelju dobrog poznavanja sastava brojeva od deset, možete dijelove oduzeti tim redoslijedom: stotine, desetke, jedinice.
Možete se množiti i dijeliti bez problema, znajući tablicu množenja - "čarobni štapić" za brzo ovladavanje računom u svom umu. Važno je napomenuti da su seoska djeca predrevolucionarne Rusije znala nastavak tzv. Pitagorejske tablice - od 11 do 19 godina, i bilo bi lijepo za moderne znanstvenike da znaju stol do 19 * 9 napamet.
Najzanimljiviji trikovi
Kako bi zarobili djecu matematikom i učinili teške trenutke u školskom kurikulumu bliže i pristupačnijim, postoje načini i metode, Pretvaranje poteškoća u zabavu i zanimljivost:
- Da biste pomnožili jednu znamenku sa 9, pokazat ćemo svima naše prazne dlanove. Savijte prst, redom (brojeći od lijeve ruke) prema broju prvog faktora. Gledamo koliko prstiju lijevo od savijenih - to će biti desetke željenog posla, a na desno - svoju jedinicu.
- Množenje od 11 bilo kojeg dvoznamenkastog broja, zbroj kojih znamenke ne dostižu 10, zabavno je i jednostavno: mentalno pomičite znamenke tog broja i stavite njihov iznos između njih - odgovor je spreman.
- Ako se zbroj znamenki pomnoženih s 11 ispostavi da je 10 ili više od 10, onda između mentalno razmaknutih znamenki tog broja trebate staviti njihovu sumu i dodati prve dvije znamenke lijevo, ostavljajući ostale dvije nepromijenjene, kako bi dobili proizvod.
Za informacije o tome kako podučiti dijete da vam odmah uzme u obzir, pogledajte sljedeći videozapis.