Hvordan lære et barn å raskt telle i tankene dine?
Foreldre til moderne barn med misunnelse ser på geeksen - deltakerne i TV-showet "Best of All" og "Amazing People" - og bekymre seg for at barna ikke skiller seg ut fra fremragende intelligens og super-humor: de behersker ikke grunnskoleprogrammet, de liker ikke å stresse sine hjerner og er redd for leksjoner matematikk.
Fra første klasse, regner de med fingre og wands, de vet ikke muntlig telling teknikker, derfor har de store problemer i alle fag i skolekurset.
Teknene for rask muntlig telling er enkle og enkle å fordøye, men det må huskes at vellykket beherskelse av dem ikke involverer mekanisk, men ganske bevisst bruk av teknikker og i tillegg mer eller mindre lang trening.
Etter å ha behersket de grunnleggende metodene for muntlig bruk, vil det være mulig å kunne utføre umiddelbare beregninger i sinnet med samme nøyaktighet som ved skriftlige beregninger, ved hjelp av dem.
funksjoner
Det er mange teknikker som fremmer læring for å fremskynde mental aritmetikk. Med alle synlige forskjeller har de en viktig likhet - de er basert på tre "hvaler":
- Opplæring og opphopning av erfaring. Regelmessig praksis, løsningen av oppgaver fra enkel til kompleks kvalitativt og kvantitativt forandre ferdigheten til oral beregning.
- Algoritme. Kunnskap og anvendelse av "hemmelige" metoder og lover gjør det enklere å telle prosessen.
- Evner og naturlige begavelser. Utviklet korttidsminne og dets store volum, samt en høy konsentrasjon av oppmerksomhet - en stor hjelp i å praktisere en rask mental aritmetikk. Et bestemt pluss er tilstedeværelsen av en matematisk tankegang og en predisposisjon til logisk tenkning.
Bruk av muntlig konto
Folk er ikke jernroboter, men det faktum at de lager smarte maskiner snakker om deres intellektuelle overlegenhet. En person må stadig holde hjernen i god form, som er aktivt fremmet av trening av ferdigheter i mental aritmetikk.
For hverdagen:
- en vellykket muntlig konto er en indikator på en analytisk tankegang;
- vanlig mental aritmetikk vil redde deg fra tidlig demens og senil marasmus;
- Din evne til å legge til og trekke godt ut vil ikke tillate deg å jukse i butikken.
For vellykket studie:
- mental aktivitet er aktivert;
- utvikle minne, tale, oppmerksomhet, evne til å oppfatte hva som ble sagt under høringen, reaksjonshastighet, oppfinnsomhet, evne til å finne de mest rasjonelle måtene for å løse oppgaven;
- styrket tillit til sine evner.
Når skal jeg starte studiene?
Ifølge de vitenskapelige sinnene (psykologer og lærere), kan et barn innen fjerde år allerede legge til og trekke fra seg. Ved en alder av 5 år kan krummen løse frie eksempler og enkle oppgaver. Men dette er statistikk, og barn tilpasser seg ikke alltid til det. derfor alt her er rent individuelt.
I alle fall er det bedre å lære barn å raskt telle i sinnet før de går inn i skolen - det blir færre problemer, og en tilførsel av nyttige ferdigheter vil bidra til å mestre moderne skoleprogrammer med større suksess.
regler
The Queen of Sciences - Matematikk - tok vare på studentene og laget et sett med lover, Algoritmer og regler, som har mestret og dyktig bruk av dem, vil barna elske matematikk og mentalt arbeid:
- Overføringsegenskapen til tillegg: Bytte komponenter av handlingen, vi får det samme resultatet.
- Den kombinerte tilleggsegenskapen: Når tre eller flere tall legges sammen, kan noen to (eller flere) tallverdier erstattes av summen deres.
- Tillegg og subtraksjon med overgangen gjennom et dusin: legg til en større komponent
- Til dusinvis av runder, og legg deretter til resten av den andre komponenten.
- Først trekker vi de enkelte enhetene fra tallet til tegnet av handlingen, og deretter fra dusinvis av runder trekker vi resten av fradragsberettiget.
- Etter å ha presentert den reduserte i form av summen av tiere og enheter, fjerner vi fra tiene av jo større den mindre og legger til svaret enhetene til den reduserende.
- Når du legger til og trekker ut dusinvis av runder (de kalles fortsatt "runde" tall), dusinvis kan betraktes som de samme som enheter.
- Tilsetning og subtraksjon av titler og enheter. Dusinvis mer praktisk å legge til dusinvis, og enheter - til enheter.
Legg til et tall til beløpet
Metodene er som følger:
- Vi beregner verdien, og vi legger til den oppgitte verdien.
- Vi legger til det i første term, og så legger vi til den andre termen til resultatet.
- Vi legger til tallet til andre sikt, og legg deretter til første sikt i svaret.
Tilsetningen av beløpet til tallet
Metodene er som følger:
- Beregn hennes vitnesbyrd, og legg deretter til nummeret.
- Vi legger til første sikt i nummeret, og deretter legger vi til andre sikt til resultatet.
- Vi legger til andre sikt til tallet, og deretter legger vi til første sikt i resultatet.
Tilsetningen av to summer. Legge til to summer, velg den mest praktiske måten å beregne.
Bruke hovedmultiplikasjonsegenskapene
Teknikkene er som følger:
- Overføringsegenskapen til multiplikasjon. Hvis vi endrer faktorene på steder, vil deres produkt ikke endres.
- Den kombinerte egenskapen til multiplikasjon. Når du multipliserer tre eller flere tall, kan to (eller flere) tall erstattes av deres produkt.
- Fordelingsegenskap av multiplikasjon. For å multiplisere summen med et tall, er det nødvendig å multiplisere hver av komponentene med dette nummeret og legge til de resulterende verkene.
Multipliser og divider tall med 10 og 100
metoder:
- For å øke et tall med 10 ganger, må du legge til ett null til høyre.
- For å gjøre det samme 100 ganger, må to nuller tildeles den til høyre.
- For å redusere tallet med 10 ganger, må du slippe ett null til høyre, og å dele med 100 - to nuller.
Multipliser beløpet med nummeret
metoder:
- Første metode. Beregn beløpet og multipliser det med denne verdien.
- Andre vei. Multipliser tallet med hver av tilleggene, og legg til de resulterende svarene.
Multipliser tall etter sum
metoder:
- Første metode. Finn summen og multipliser nummeret med det vi får.
- Andre vei. Multipliser tallet ved hver av tilleggene, og legg til de resulterende verkene.
Deler beløpet med tallet
metoder:
- Første metode. Beregn beløpet og del det med et tall.
- Andre vei. Hver av tilleggene er delt med tallet og de resulterende kvotientene blir lagt til.
Deler nummeret på produktet
alternativer:
- Første metode. Del tallet med den første faktoren, og del deretter resultatet med den andre faktoren.
- Andre vei. Del tallet med den andre faktoren, og del deretter resultatet med den første faktoren.
typer
I løpet av leksjonene tildeles sparsom tid til munnkontoen, men dette forringer ikke dets betydning for utviklingen av barns mentale aktivitet. Mundtlige beregningsfag blir dannet i matematikkleksjonene i grunnskolen når du utfører ulike typer oppgaver og øvelser.
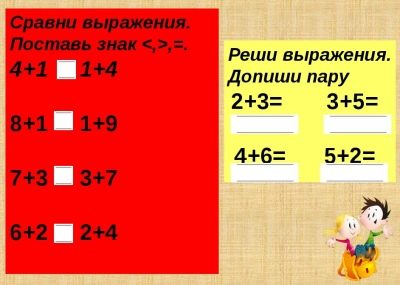
Finn verdien av et matteuttrykk
Disse kan være vanlige numeriske uttrykk eller uttrykk med en variabel (alfabetisk), og numeriske verdier foreslås for bokstaver.Ved å erstatte tallene i stedet for bokstaver, finn tallverdien av det resulterende uttrykket.
Sammenlign matematikkuttrykk
Slike oppgaver er varierte:
- bestemme likestilling eller ulikhet av de to gitt uttrykkene (har tidligere funnet og sammenlignet sine verdier);
- til forholdet som er gitt til tegnet og et av uttrykkene for å komponere det andre uttrykket eller for å fullføre den uferdige foreslåtte
- I slike øvelser kan enkeltsifrede, tosifrede, tresifrede tall og mengder brukes i uttrykk og alle fire aritmetiske operasjoner. Hovedformålet med slike oppgaver er solid mastering av teoretisk materiale og utvikling av beregningsmessige ferdigheter.
- Løs ligningen. De bidrar til å forstå forholdet mellom komponenter og resultatene av aritmetiske operasjoner.
- Løs problemet. Disse kan være både enkle og komplekse oppgaver. Med deres hjelp blir teoretisk kunnskap styrket, beregningsmessige ferdigheter og ferdigheter utviklet, barns mentale aktivitet er aktivert.
Orale konto mottakelser
Tegn på delbarhet av tall:
- med 2: alt som overskrider det, og i den numeriske serien går gjennom en;
- på 3 og 9: hvis summen av tallene er et flertall av disse indikatorene uten en balanse;
- ved 4: hvis de to siste sifrene i posten suksessivt danner et tall som er delt med 4;
- 5: runde dusinvis og de der det er 5 på slutten;
- ved 6: tall som er multipler av to og tre er delt;
- 10: numeriske verdier, der posten er på slutten er 0;
- 12: Del tallene som kan deles inn i tre og fire på samme tid;
- med 15: tall som er delt samtidig av enkeltverdierte heltallskomponenter av dette nummeret er multiplikatorer.
Grunnskole kontoskjemaer
Det er velkjent at hovedaktiviteten til barnehager og yngre studenter er et spill som er nyttig å inkludere i alle stadier av leksjonen. Noen former for muntlig konto vil bli gitt nedenfor.
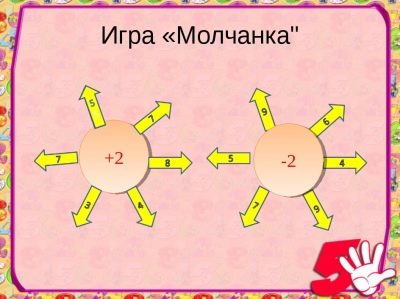
Spillet "Silent"
Fremmer oppmerksomhet og disiplinutdanning. En stillhet kan bestå av eksempler i en handling, to eller flere. Det spilles i alle klasser av grunnskolen med både abstrakte heltall og navngitte numre.
Studentene vurderer i sine tanker og stille stille på lærerne skrive svarene på eksemplene som tilbys dem på tavlen. De riktige svarene blir møtt med lette klapper og feil svar med stillhet.
Spill "Lotto"
Det kan være flere typer som svarer til de delene av matematikk som studeres og må løses. For eksempel, lotto med eksempler på multiplikasjon og divisjon innenfor "hundrevis".
For å gi mer interesse for spillet, kan dekk med svar gjøres fra et snittbilde. Hvis alle eksemplene er løst på riktig måte, blir det laget et bilde fra dekkene.
Spill "Aritmetiske labyrinter"
De ser ut som konsentriske sirkler med porter med tall. For å komme til sentrum må du ringe et nummer i sentrum. Labyrinter for løsningen kan kreve enten en handling (tillegg) eller flere. Det skal bemerkes at disse oppgavene har flere løsninger.
Spillet "Fang piloten" (en slags "stige")
På tegnebrettet: et fly med løkker, i hvilke eksempler. To påkalte studenter registrerer svar til venstre og høyre på løkkene. Hvem bestemmer seg riktig og raskt, vil han komme opp med piloten.
Spillet "Sirkulære eksempler"
Det didaktiske materialet er et sett med kort, arrangert i konvolutter; Hver av dem har 8 kort, som hver inneholder ett eksempel.
De numeriske eksemplene i hver konvolutt er forskjellige i innholdet og er valgt i henhold til selvkontrollens prinsipp: Når de løses, blir resultatet av et eksempel begynnelsen av det neste.
Sirkulære eksempler kan tilbys som stiger.
Metoder og teknikker for utvikling
Med tanke på måtene å undervise barn på 6 år for å raskt telle i sinnet, er det umulig å ikke merke seg den unike og enkelheten i den japanske metoden for å telle "Soroban". Med "Soroban" -metoden kan du trene barn i alderen 4 til 11 år, utvikle sine mentale evner og utvide spekteret av intellektuelle evner hos barn.Det er lett å lære noen skolebarn å ta eksempler på matematikk i sinnet ved å bruke den japanske metoden for sorobantelling. Ved å praktisere mentale verbale teller setter vi hele hjernen i drift., og dermed losser venstre halvkule, som er ansvarlig for å løse matematiske problemer.
Mental aritmetikk tillater selv den "figurative" halvkule å være interessert i beregningsoperasjoner, noe som øker effektiviteten til hjernen.
Stort antall krever skriftlige beregningsmetoder, selv om det finnes personer som finpusser sine ferdigheter i å jobbe med dem.
Å lese matematiske eksempler i sinnet er en viktig nødvendighet, siden eksamener på skolen er nå uten bruk av kalkulatorer, og evnen til å telle i sinnet er inkludert i listen over obligatoriske ferdigheter for kandidater på 9 og 11 karakterer.
Den grunnleggende regelen for mentalt tillegg er:
- Hvis første termen er et tosifret tall (ikke et runde dusin), legg deretter til 9 til det som følger: Legg til 10, fjern 1.
- Legg til 8: legg til 10, fjern 2.
Legg raskt til tosifrede tall:
- Hvis det siste sifferet i andre sikt er større enn 5, runde det opp. Utfør tillegg, fjern "additivet" fra mottatt beløp.
- Hvis det siste sifferet i det andre begrepet er mindre enn 5, legger du deretter opp med siffer: Først legger du til dusinvis, deretter - enheter.
- Du kan bytte vilkårene på steder, men legg til tallene med samme algoritme.
Subtraksjon funksjoner: reduksjon til runde tall
Utvetydig fradragsberettiget er avrundet til 10, tosifret - opptil 100. Trekk 10 eller 100 og legg til endringen. Resepsjonen er relevant for små endringer.
Trekk tresifrede tall i tankene
Basert på god kunnskap om sammensetningen av tallene på de ti, kan du trekke i deler i denne rekkefølgen: hundrevis, titalls, enheter.
Du kan multiplisere og dele uten problemer ved å kjenne multiplikasjonstabellen - "magic wand" for raskt å mestre kontoen i tankene dine. Det er bemerkelsesverdig at landsbyens barn i pre-revolusjonerende Russland kjente fortsettelsen av det såkalte Pythagorean-bordet - fra 11 til 19, og det ville være fint for moderne lærde å kjenne bordet opp til 19 * 9 av hjertet.
De mest interessante triksene
Å fange barn med matematikk og gjøre vanskelige øyeblikk i skolens læreplan nærmere og mer tilgjengelig, det er måter og metoder, Snu vanskeligheter til morsomt og interessant:
- For å multiplisere et enkelt siffer med 9, la oss vise alle våre tomme palmer. Bøy fingeren, tilsvarende i rekkefølge (teller fra tommelen til venstre) til nummeret til den første faktoren. Vi ser på hvor mange fingre til venstre for bøyden - det vil være dusinvis av ønsket arbeid, og til høyre - sin egen enhet.
- Multiplikasjon med 11 av et tosifret tall, summen av hvilke siffer som ikke kommer til 10, er morsomt og enkelt: Beveg sifferene i dette nummeret mentalt og legg summen mellom dem - svaret er klart.
- Hvis summen av tallene multiplisert med 11 viser seg å være 10 eller mer enn 10, så mellom de mentalt flyttede tallene i dette nummeret, bør du sette summen deres og legge de to første sifrene til venstre, slik at de to andre blir uendrede, for å få produktet.
For informasjon om hvordan du lærer et barn å umiddelbart telle i tankene dine, se følgende video.