Hoe leer je een kind om snel in je hoofd te tellen?
Ouders van moderne kinderen met jaloezie kijken naar de geeks - deelnemers aan de televisieshow "Best of All" en "Amazing People" - en vrezen dat hun kinderen niet onderscheiden worden vanwege hun buitengewone intelligentie en super-humor: ze leren het basisschoolprogramma slecht, ze houden niet van hun hersens en zijn bang voor lessen wiskunde.
Vanaf de eerste klas rekenen ze op vingers en toverstokken, ze kennen geen orale teltechnieken, daarom hebben ze grote problemen in alle vakken van de schoolopleiding.
De technieken van snel mondeling tellen zijn eenvoudig en gemakkelijk verteerbaar, maar er moet aan worden herinnerd dat het succesvol beheersen ervan geen mechanisch, maar redelijk bewust gebruik van technieken en, bovendien, min of meer langdurige training impliceert.
Na het beheersen van de elementaire methoden van mondelinge account, zullen ze in staat zijn om direct en snel directe berekeningen in de geest uit te voeren met dezelfde nauwkeurigheid als met geschreven berekeningen.
Speciale functies
Er zijn zoveel technieken die leren bevorderen om hoofdrekenen te bespoedigen. Met alle zichtbare verschillen hebben ze een belangrijke gelijkenis - ze zijn gebaseerd op drie "walvissen":
- Opleiding en accumulatie van ervaring. Regelmatige praktijk, de oplossing van taken van eenvoudig tot complex, kwalitatief en kwantitatief de vaardigheid van mondelinge berekening te veranderen.
- Algoritme. Kennis en toepassing van 'geheime' methoden en wetten vereenvoudigt het tellen aanzienlijk.
- Capaciteiten en natuurlijke gaven. Ontwikkeld kortetermijngeheugen en zijn aanzienlijke volume, evenals hoge concentratie van aandacht - een grote hulp bij het oefenen van een snelle hoofdrekenen. Een absoluut pluspunt is de aanwezigheid van een wiskundige instelling en een aanleg voor logisch denken.
Het gebruik van het mondelinge account
Mensen zijn geen ijzeren robots, maar het feit dat ze slimme machines maken, spreekt van hun intellectuele superioriteit. Een persoon moet voortdurend zijn brein in goede conditie houden, wat actief wordt bevorderd door het trainen van vaardigheden in hoofdrekenen.
Voor het dagelijks leven:
- een succesvol mondeling verslag is een indicator van een analytische mindset;
- regelmatige hoofdrekenen zal je redden van vroege dementie en seniele marasmus;
- je vermogen om goed toe te voegen en af te trekken laat je niet toe om vals te spelen in de winkel.
Voor een succesvolle studie:
- mentale activiteit is geactiveerd;
- geheugen ontwikkelen, spraak, aandacht, vermogen om te zien wat er op de hoorzitting werd gezegd, snelheid van reactie, vindingrijkheid, het vermogen om de meest rationele manieren te vinden om het probleem op te lossen;
- versterkt vertrouwen in hun capaciteiten.
Wanneer moet ik beginnen met mijn studie?
Volgens de geoefende geest (psychologen en opvoeders) kan een kind tegen het 4e jaar al toevoegen en aftrekken. Op de leeftijd van 5 jaar kan de kruimel vrijelijk voorbeelden en eenvoudige taken oplossen. Maar dit zijn statistieken en kinderen passen zich er niet altijd aan aan. daarom Alles hier is puur individueel.
In ieder geval is het beter om kinderen te leren snel in hun gedachten te tellen voordat ze naar school gaan - er zullen minder problemen zijn en een aanbod van nuttige vaardigheden zal helpen moderne schoolprogramma's beter te beheersen.
reglement
De Koningin van Wetenschappen - Wiskunde - zorgde voor de studenten en maakte een reeks wetten, Algoritmen en regels, na deze te hebben beheerst en vakkundig te gebruiken, zullen kinderen dol zijn op wiskunde en mentaal werk:
- De overdrachtseigenschap van optellen: het verwisselen van de componenten van de actie, we krijgen hetzelfde resultaat.
- De eigenschap gecombineerde toevoeging: wanneer drie of meer getallen bij elkaar worden opgeteld, kunnen twee (of meer) numerieke waarden worden vervangen door hun som.
- Optellen en aftrekken met de overgang door een dozijn: voeg een groter component toe
- Om tientallen rondes, en voeg dan de rest van de andere component.
- Trek eerst de individuele eenheden van het getal af tot het teken van de actie en vervolgens van de tientallen rondes trekken we de rest van het eigen risico af.
- Nadat we de verminderde hebben gepresenteerd in de vorm van de som van tientallen en eenheden, verwijderen we van de tientallen van de grotere de kleinere en voegen we aan het antwoord de eenheden van de afnemende toe.
- Bij het optellen en aftrekken van tientallen rondes (ze worden nog steeds "ronde" getallen genoemd), kunnen tientallen hetzelfde worden beschouwd als eenheden.
- Optellen en aftrekken van tientallen en eenheden. Tientallen handiger om aan de tientallen en eenheden toe te voegen aan eenheden.
Een getal aan de som toevoegen
De methoden zijn als volgt:
- We berekenen de waarde ervan en voegen deze waarde eraan toe.
- We voegen het toe aan de eerste term en vervolgens voegen we de tweede term aan het resultaat toe.
- We voegen het nummer toe aan de tweede term en voegen vervolgens de eerste term toe aan het antwoord.
De toevoeging van het bedrag aan het aantal
De methoden zijn als volgt:
- We berekenen zijn getuigenis en dan voegen we het toe aan het nummer.
- We voegen de eerste term toe aan het nummer en vervolgens voegen we de tweede term aan het resultaat toe.
- We voegen de tweede term toe aan het nummer en vervolgens voegen we de eerste term aan het resultaat toe.
De toevoeging van twee sommen. Door twee sommen toe te voegen, kiezen we de gemakkelijkste manier om te berekenen.
De belangrijkste eigenschappen van vermenigvuldiging gebruiken
De technieken zijn als volgt:
- De overdrachtseigenschap van vermenigvuldiging. Als we de factoren op plaatsen wijzigen, zal hun product niet veranderen.
- De gecombineerde eigenschap van vermenigvuldiging. Bij het vermenigvuldigen van drie of meer nummers, kunnen twee (of meer) nummers worden vervangen door hun product.
- Distributie-eigenschap van vermenigvuldiging. Om de som met een getal te vermenigvuldigen, is het noodzakelijk om elk van zijn componenten met dit aantal te vermenigvuldigen en de resulterende werken toe te voegen.
Vermenigvuldig en deel nummers met 10 en 100
methoden:
- Als u een getal tien keer wilt vergroten, moet u een nul toevoegen aan de rechterkant.
- Om dit 100 keer te doen, moeten er aan de rechterkant twee nullen aan worden toegewezen.
- Als u het aantal tien keer wilt verkleinen, moet u één nul naar rechts laten vallen en vervolgens met 100 - twee nullen.
Vermenigvuldig het bedrag met het nummer
methoden:
- 1e methode. Bereken de hoeveelheid en vermenigvuldig deze met deze waarde.
- 2e manier. Vermenigvuldig het aantal met elk van de bijlagen en voeg de ontvangen antwoorden toe.
Vermenigvuldig aantal bij som
methoden:
- 1e methode. Zoek de som en vermenigvuldig het aantal wat we krijgen.
- 2e manier. Vermenigvuldig het aantal met elk van de bijlagen en voeg de resulterende werken toe.
De hoeveelheid delen door het aantal
methoden:
- 1e methode. Bereken de hoeveelheid en deel deze door een cijfer.
- 2e manier. Elk van de bijlagen wordt gedeeld door het nummer en de resulterende quotiënten worden toegevoegd.
Het nummer van het product verdelen
opties:
- 1e methode. Deel het aantal met de eerste factor en deel het resultaat vervolgens met de tweede factor.
- 2e manier. Deel het aantal met de tweede factor en deel het resultaat vervolgens met de eerste factor.
types
Tijdens de lessen op het mondelinge verslag wordt weinig tijd gegeven, maar dit neemt niet weg dat het van belang is voor de ontwikkeling van de mentale activiteit van kinderen. Verbale computervaardigheden worden gevormd in de wiskundelessen op de basisschool bij het uitvoeren van verschillende soorten taken en oefeningen.
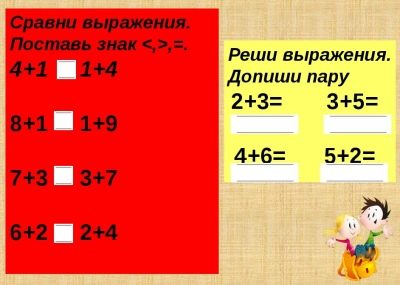
Zoek de waarde van een wiskundige uitdrukking
Dit kunnen gewone numerieke uitdrukkingen of uitdrukkingen zijn met een variabele (alfabetisch), en numerieke waarden worden voorgesteld voor letters.Vervangen van getallen in plaats van letters, vindt de numerieke waarde van de resulterende expressie.
Vergelijk Math Expressions
Dergelijke taken zijn gevarieerd:
- bepalen van de gelijkheid of ongelijkheid van deze twee uitdrukkingen (na het vinden en vergelijken van hun waarden);
- naar de relatie die aan het teken wordt gegeven en een van de uitdrukkingen om de tweede uitdrukking samen te stellen of om de onvoltooide voorgestelde af te ronden;
- in dergelijke oefeningen kunnen ééncijferige, tweecijferige, driecijferige getallen en hoeveelheden worden gebruikt in uitdrukkingen en alle vier rekenkundige bewerkingen. Het hoofddoel van dergelijke taken is een degelijke assimilatie van theoretisch materiaal en de ontwikkeling van computervaardigheden.
- Los de vergelijkingen op. Ze helpen de verbindingen tussen componenten en de resultaten van rekenkundige bewerkingen te begrijpen.
- Los het probleem op. Het kunnen zowel eenvoudige als complexe taken zijn. Met hun hulp wordt de theoretische kennis versterkt, computationele vaardigheden en vaardigheden ontwikkeld, de mentale activiteit van kinderen geactiveerd.
Orale accountrecepties
Tekenen van deelbaarheid van nummers:
- door 2: alles dat het overschrijdt, en in de numerieke rij door één gaat;
- op 3 en 9: als de som van de cijfers een veelvoud is van deze indicatoren zonder een balans;
- door 4: als de laatste twee cijfers in de record achtereenvolgens een getal vormen dat wordt gedeeld door 4;
- 5: ronde tientallen en die waarbij er 5 aan het einde is;
- met 6: getallen die veelvouden van twee en drie zijn, zijn verdeeld;
- 10: numerieke waarden, waarbij de record aan het einde is 0;
- 12: deel de nummers die op hetzelfde moment in drie en vier kunnen worden verdeeld;
- op 15: getallen die op hetzelfde moment worden opgedeeld in integrale enkelwaardige componenten van dit aantal factoren.
Basisschool account formulieren
Het is bekend dat de hoofdactiviteit van kleuters en jongere studenten een spel is dat nuttig is om in alle stadia van de les op te nemen. Hieronder worden enkele vormen van het mondelinge account weergegeven.
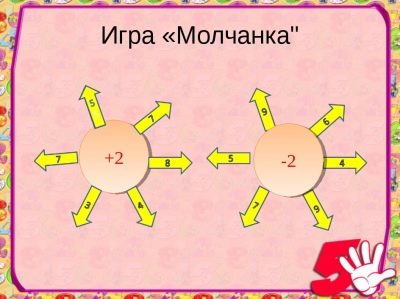
Het spel "Silent"
Het helpt om aandacht en discipline te cultiveren. Een stilte kan bestaan uit voorbeelden in één actie, twee of meer. Het wordt gespeeld in alle klassen van de basisschool met zowel abstracte gehele getallen als benoemde nummers.
De studenten bekijken in gedachten en roepen op zwijgende toon de leraren de antwoorden op de voorbeelden die ze op het bord krijgen aangeboden. De juiste antwoorden worden voldaan met lichte klappen en de foute antwoorden met stilte.
Game "Lotto"
Er kunnen verschillende typen zijn die overeenkomen met die delen van de wiskunde die zijn bestudeerd en moeten worden geconsolideerd. Bijvoorbeeld lotto met voorbeelden van vermenigvuldiging en verdeling binnen de "honderden".
Om meer interesse in het spel te krijgen, kunnen banden met antwoorden worden gemaakt van een gesneden foto. Als alle voorbeelden correct zijn opgelost, wordt een foto gemaakt van de banden.
Spel "Rekenkundige labyrinten"
Ze zien eruit als concentrische cirkels met poorten met cijfers. Om naar het midden te gaan, moet je een nummer in het midden bellen. Labyrinten voor de beslissing kunnen één actie (toevoeging) of meerdere vereisen. Opgemerkt moet worden dat deze taken verschillende oplossingen hebben.
Het spel "Catch the pilot" (een soort van "ladder")
Op de tekentafel: een vlak met lussen, in welke voorbeelden. Twee opgeroepen studenten nemen de antwoorden links en rechts van de loops op. Wie beslist en snel beslist, zal de piloot inhalen.
Het spel "Circular Examples"
Didactisch materiaal is een set kaarten, gerangschikt in enveloppen; Elk van hen heeft 8 kaarten, die elk een voorbeeld bevatten.
De numerieke voorbeelden in elke envelop zijn verschillend qua inhoud en worden geselecteerd volgens het principe van zelfbeheersing: bij het oplossen ervan is het resultaat van een voorbeeld het begin van het volgende.
Circulaire voorbeelden kunnen als ladders worden aangeboden.
Methoden en technieken voor ontwikkeling
Gezien de manieren om kinderen van 6 jaar en ouder te leren snel te tellen, is het onmogelijk om de uniekheid en eenvoud van de Japanse methode om "Soroban" te tellen niet op te merken. Met de Soroban-techniek kun je kinderen van 4 tot 11 jaar trainen, hun mentale vermogens ontwikkelen en het scala aan intellectuele capaciteiten van kinderen vergroten.Het is gemakkelijk om elke student te leren voorbeelden van wiskunde in de geest te nemen, met behulp van de Japanse methode om op sorobane te rekenen. Door het oefenen van mentale verbale tellingen, zetten we de hele hersenen in werking., waardoor de linker hemisfeer wordt gelost, die verantwoordelijk is voor het oplossen van wiskundige problemen.
Met mentale rekenkunde kan zelfs het "figuratieve" halfrond worden geïnteresseerd in computationele operaties, wat de efficiëntie van de hersenen verhoogt.
Grote aantallen vereisen geschreven berekeningsmethoden, hoewel er mensen zijn die hun vaardigheden bij het werken met hen aanscherpen.
Het beschouwen van voorbeelden van wiskunde in de geest is een essentiële noodzaak, sinds examens op school zijn nu zonder het gebruik van rekenmachines, en het vermogen om te tellen in de geest is opgenomen in de lijst van verplichte vaardigheden van afgestudeerden van 9 en 11 graden.
De basisregel voor mentale toevoeging is:
- Als de eerste term een tweecijferig getal is (geen ronde dozijn), voegt u er als volgt 9 toe: voeg 10 toe, verwijder 1.
- Voeg 8 toe: voeg 10 toe, verwijder 2.
Voeg snel tweecijferige nummers toe:
- Als het laatste cijfer van de tweede term groter is dan 5, moet u het naar boven toe afronden. We voeren de toevoeging uit, uit het resulterende bedrag verwijderen we het "additief".
- Als het laatste cijfer van de tweede term kleiner is dan 5, tel dan op met cijfers: eerst, tel tientallen, dan - eenheden.
- U kunt de voorwaarden op plaatsen omwisselen, maar de nummers met hetzelfde algoritme toevoegen.
Aftrekfuncties: verkleinen tot ronde getallen
Ondubbelzinnig eigen risico is afgerond op 10, tweecijferig - maximaal 100. Trek 10 of 100 af en voeg het amendement toe. Receptie is relevant voor kleine wijzigingen.
Trek driecijferige getallen in gedachten
Gebaseerd op een goede kennis van de samenstelling van de getallen van de tien, kun je in delen in deze volgorde aftrekken: honderden, tientallen eenheden.
Vermenigvuldigen en delen kan gemakkelijk zijn, wetende de tafel van vermenigvuldiging - "toverstaf" naar de snelle ontwikkeling van het account in de geest. Het is opmerkelijk dat de dorpskinderen van het pre-revolutionaire Rusland de voortzetting van de zogenaamde Pythagorean-tafel kenden - van 11 tot 19, en het zou leuk zijn voor moderne geleerden om de tafel tot 19 * 9 uit hun hoofd te kennen.
De meest interessante trucs
Om kinderen te boeien met wiskunde en de moeilijke momenten in het leerplan van de school dichterbij en toegankelijker te maken, zijn er manieren en methoden, Moeilijkheden veranderen in leuk en interessant:
- Om elk enkel cijfer met 9 te vermenigvuldigen, laten we iedereen onze lege handpalmen tonen. Buig uw vinger, corresponderend in volgorde (te rekenen vanaf de duim van de linkerhand) tot het cijfer van de eerste factor. We kijken naar hoeveel vingers links van de gebogen - het zullen tientallen van het gewenste werk zijn, en aan de rechterkant - zijn eigen eenheid.
- Vermenigvuldiging met 11 van elk getal van twee cijfers, waarvan de som niet 10 bereikt, is leuk en eenvoudig: verplaats de cijfers van dit getal en zet hun som ertussen - het antwoord is klaar.
- Als de som van de getallen vermenigvuldigd met 11 10 is of meer dan 10, moet u tussen de mentaal gespatieerde cijfers van dit getal de som plaatsen en de eerste twee cijfers links toevoegen, terwijl de andere twee ongewijzigd blijven om het product te krijgen.
Zie de volgende video voor informatie over hoe u uw kind kunt leren om direct in uw gedachten te tellen.